-
Notifications
You must be signed in to change notification settings - Fork 5
The FALCON functions
Network building and decomposition: Once the network structure and experimental data files are assigned. Users can apply the function “FalconMakeModel” to extract information from the model and data files and stored them into the variable called “estim”. Within the “FalconMakeModel” function, the network might be expanded by the function “FalconExpand” to decompose complex non-linear interactions into simplified interactions which can be optimised faster by the FALCON framework. Note that the expanded model description can also be saved into a text file by the function “FalconInt2File” if needed.
Parameter initialisation and model optimisation: The “estim” variable carries all essential information for model optimisation. Model optimisation is a process of identifying parameter values in the model which make the models fit to experimental data. Prior to the optimisation process, users can choose between the two types of distribution to initialise parameter values, either a uniform distribution (default) or a normal/Gaussian distribution, as well as to assign the S.D. of the normal distribution in the latter case. Then, the initialised parameters together with “estim” are passed into the optimisation process in the next step.
Optimiser and the updating scheme: we apply the Matlab built-in optimiser “fmincon” within the function “FalconObjFun” to perform parameter optimisation. “fmincon” uses gradient descent to find the set of optimised parameters which returns the state values of the outputs in the model that match best the experimental data. In the current implementation, we focus on the optimisation of the model against steady-state data so we simulate/update the system with a set of parameters until all node values reach steady-state. In our definition, the steady-state is reached when the sum of the squared differences between the simulated state values from all nodes between two updates is less than a very low threshold (default value is ‘eps’, i.e. 2.2x10-16). The differences between the simulated state values from the model and the experimental data are then expressed by the sum-of-square error (SSE) between the model simulations and the data across all experimental conditions.
Parallel computing: to acquire a distribution of optimised parameter values and fitting costs, multiple rounds of parameter optimisation are required. To speed-up this process, the FALCON pipeline is compatible with the Matlab built-in Parallelisation Toolbox. This is convenient for machines with multiple CPU cores or for a computational cluster. Note that the progress bar will not be displayed in the parallel computing mode.
Summarisation of optimisation results: a summary of the optimisation results can be displayed on the Matlab command window by calling the function “FalconResults”. After each run, the list of optimised parameters is automatically saved in a folder. Furthermore, the evolution of the fitting course during the optimisation process can be displayed as a figure by calling the function “FalconFitEvol”. A number of useful plots allowing the assessment of the model fitting quality can also be called via the function “FalconSimul”. Finally, the network graph with molecular activities at steady-state and the optimised parameter values can be displayed in the form of Matlab’s Biograph by executing the function “FalconShowNetwork”. This feature requires a lot of memory and should be disabled when analysing large datasets.
The calculation of the optimal costs in the FALCON pipeline (via SSE) only considers the average value for each experimental point. The function “FalconResample” allows to take experimental variations into consideration. The resampling analysis starts from the resampling of artificial datasets based on the mean and S.D. of the data which are assumed to be normally distributed. The number of new datasets sampled and the number of optimisation rounds can be defined on the variables “New_Data_Sampling” and “optRound_Sampling”, respectively. Then, multiple rounds of optimisation are performed against the artificial datasets and the distribution of the optimised parameters is analysed. The users can also choose an arbitrary cut-off of coefficient of determination (CV), to determine if the obtained optimised parameter values are robust against the variations within the experimental observations.
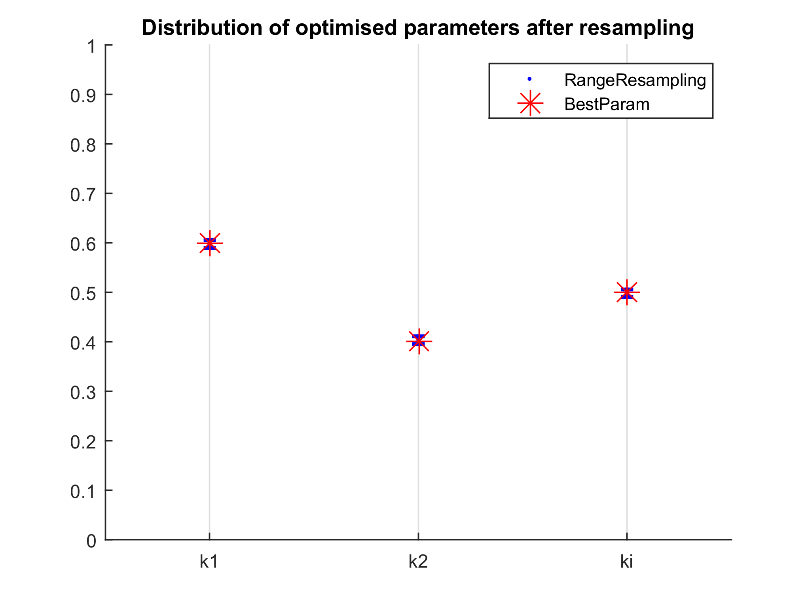
The resampled parameter values based on the mean and the standard deviation. The figures correspond to the new artificial datasets created based on the experimental data.
To assess whether the optimised parameters are identifiable or not, we offer a local parameter sensitivity analysis (LPSA) pipeline within the function “FalconLPSA”. The analysis consists in the evaluation of the model under a set of parametrisations in which each parameter is perturbed over the range of possible values while the other ones are free. A plot is then generated to show the fitness landscape of the model along the dimension of each of the parameters. A flat curve indicates that the parameter is not identifiable. To speed up calculations, we focus the analysis around the optimal values and first perform the resampling analysis as described in (3.) to define a cut-off value which determines when the fit is significantly worse than the optimal model.

The figure displays the different parameters of the model. From the optimal parameter set (blue star), each parameter is perturbed in the direction of the upper and lower bound. The perturbed parameter value is fixed and all the other parameters are re-optimized. The red line corresponds to the cut-off calculated by the resampling.
Biological networks derived from prior knowledge, literature, or databases, are likely to contain both essential and non-essential interactions which could explain the experimental data, depending on the cellular context. To evaluate if a certain interaction is essential in the context of the study, the users can apply the function “FalconKO” in order to re-optimize the model with the respective interaction removed. In the KO analysis, the function first creates a set of model variants in which one interaction has been removed. Then, the optimisation is performed to get a new optimal cost. In order to obtain a robust estimate which has a good balance between the fitting cost and the degree of freedom (i.e. number of parameters), we use the Akaike Information Criteria (AIC) (cite:Akaike1974, cite:Burnham2001) as the indicator for the assessment. The interaction is defined as essential in the KO study if the AIC value of the model variant with a knocked-out interaction has higher AIC value than the optimal model while the interaction is defined as non-essential otherwise.

The figure displays the obtained results for the knock-out analysis. The AIC for the reference model is colored in blue. Parameters having an effect on the model optimization after removal are displayed in black. Parameters having no effect on the model optimization after removal are displayed in green (not shown here).
If the experimental data is partitioned into training and validation datasets, the script “FalconValidation” can be used to test the performance of the trained model. The model is evaluated against the new conditions and the predictions of the model can then be visualised in a plot against the validation datasets whether the predicted state values match the validation dataset within its error range.
It is often the case that a biological experiment consists of the measurement of different analytes under different experimental conditions, in different contexts. The contexts can be different cell lines, patients, or different time points. Such a setup is required to consider different versions of the model to account for differential regulation between contexts. However some interactions might be assumed to be identically parametrised in all contexts.
We provide the function “FalconMakeGlobalModel” which builds a meta-model comprising all interactions and parameters for all contexts, including the ones that are common between contexts and the ones that are ‘localized’ i.e. which are specific to one of the contexts.
We provide the driver script “DriverFalconDiff” which guides the users into the analysis of such models. The necessary files are the model definition file, a list of the fixed interactions (in the same formatting as the model file), and a number of measurement files corresponding to the different contexts. A toy model is included as example file.