Skip to content
/ thermopack Public

Thermopack is a thermodynamic model library for fluid properties and PVT calculations

License

Unknown, MIT licenses found

Licenses found

Unknown
LICENSE-APACHE
MIT
LICENSE-MIT
54 stars 13 forks Branches Tags Activity
Star
Notifications You must be signed in to change notification settings

thermotools/thermopack

BranchesTags

Repository files navigation

ThermoPack homepage

For the full documentation and user guide to ThermoPack, see the ThermoPack homepage. If you are running ThermoPack installed via pip, make sure to check the documentation for the correct version by selecting the version number in the sidebar.

About

Thermopack is a thermodynamics library for multi-component and multi-phase thermodynamics developed at SINTEF Energy Research and NTNU Department of Chemistry. Through decades of research, we have developed a software that performs thermodynamic calculations. A large selection of equations of state has been implemented in this software. Most of these equations of state have been developed by other research groups around the world, but some of them have been developed by us. Thermopack has been a much-appreciated in-house powerhouse.

Thermopack is available for everybody, free of charge under the MIT/Apache 2.0 open-source licenses. Thermopack is written in FORTRAN to handle heavy numerical computations associated with process and computational fluid dynamics (CFD) simulations. The thermodynamic framework is easily interfaced from C/C++ and also contains a flexible Python wrapper to make scripting easy.

Table of contents

Please Cite

Thermopack has been developed through many projects, and have produced many articles. If you are writing academic publications, please cite one or more of the following articles:

License

Thermopack is distributed under the MIT license and Apache 2.0.

Acknowledgments

A number of colleagues at SINTEF Energy Research and NTNU have contributed to the development of thermopack. We gratefully acknowledge their contributions.

Program structure

Each EoS in thermopack is a class, which inherits from the thermopack class found in thermo.py. The primary documentation for the thermopack python wrapper consists of the docstrings of the thermopack class. This class contains all generic methods used to compute thermodynamic properties, phase equilibria, etc. The inheriting classes simply ensure that the correct part of the Fortran-module is linked when performing calculations, and provide some extended functionality for handling EoS parameters and such. See the wiki for more information on this.

Fluid parameters are compiled into the Fortran-module, and are not directly accessible through the Python-wrapper. The entire fluid parameter database used by thermopack may be found in the /fluids directory in the GitHub repo. In order to model fluids not currently supported in the module available through pip, thermopack must be compiled from source with the new parameters. See the wiki for information on how to add new fluids, and the GitHub README for a guide on how to compile from source. Please feel free to leave a PR for new parameter sets such that these can be included in future releases of thermopack.

File System

Brief description of file structure:

  • thermopack/: Main library folder containing make scripts etc.
  • thermopack/src/: Main path for Fortran source code
  • thermopack/unittest/: Test files written for pFUunit
  • thermopack/bin/: Compiled binaries and libraries
  • thermopack/doc/: Memos and doxygen documentation
  • thermopack/fluids/: Pure fluid files
  • thermopack/binaries/: Files containing binary interaction parameters etc.
  • thermopack/MSVStudio/: Microsoft Visual Studio project and solution files
  • thermopack/include/: C/C++ include file
  • thermopack/pyplot/: Example plot-scripts (Plotting text files generated by Thermopack)
  • thermopack/addon/: Add-on functionality
  • thermopack/addon/pycThermopack/: Python interface
  • thermopack/addon/pyUtils/: Python utilities for generating fortran code and makefile input.
  • thermopack/addon/trend_interface/: Interface for working with the TREND/EOSCG library developed by Roland Span and Ruhr-Universität Bochum

Installing the latest version of ThermoPack

Using pip

Thermopack has been compiled for Windows, Linux and macOS and made available on the Python Package Index (pypi), and can be installed using pip

pip3 install thermopack

For documentation on the version available on pypi, refer to the appropriate version number in the sidebar.

Installing from wheels

Pre-built wheels for the latest version of ThermoPack on GitHub are available for download here. Refer to the linked page for instructions on how to install packages directly from a python wheel. Please note that the latest version on GitHub may be less stable, tested, and well documented than the versions distributed on PyPI.

Building from source

The following sections show how to fetch, compile and install Thermopack and the Python frontend pycThermopack. When things are properly installed, it may be useful to look into the examples provided in the getting started guide, and the pyExamples.

Prerequisites

Thermopack source code can be compiled with the GNU Fortran compiler or Intel FORTRAN and is dependent on the LAPACK and BLAS libraries. On the Windows OS the code can be compiled using Microsoft Visual Studio. A solution file is found in thermopack/MSVStudio, assuming that the Intel Fortran compiler is integrated with Microsoft Visual Studio.

For macOS and Linux, Lapack and Blas can likely be installed using apt, brew, or similar. For windows, Lapack will need to be built from source. The CMake setup for Windows is configured to handle this automatically.

CMake setup (macOS and Linux)

The cmake-based build system assumes that you have Lapack and gfortran installed, see above instructions for more on that.

Build and install thermopack by running

mkdir build
cd build
cmake ..
make install

This will ensure that the thermopack dynamic library is properly installed to thermopack/installed and thermopack/addon/pycThermopack/thermopack.

To set up the python wrapper,

python addon/pycThermopack/map_platform_specifics.py
pip install addon/pycThermopack/

this will generate the file addon/pycThermopack/thermopack/platform_specifics.py and install thermopack to your activated virtual environment.

ThermoPack can be configured to return computed properties as either tuples (v2) or using the Property struct (v3), this is toggled with the -diffs flag when running map_platform_specifics.py as

python map_platform_specifics.py --diffs=v2 # Use tuples
python map_platform_specifics.py --diffs=v3 # use Property

the default value is --diffs=v3. After running this command you should recieve a confirmation message that thermopack was successfully configured.

CMake setup (Windows)

To compile thermopack (and Lapack) with Intel FORTRAN and MSVS, first run

git submodule update --init --recursive

from within the thermopack direcory, in order to clone Lapack. Then, run

mkdir build
cd build
cmake .. -DCMAKE_Fortran_COMPILER=ifort -DCMAKE_BUILD_TYPE=Release
cmake --build . --config=Release --target install

Compile and install Lapack, and install the thermopack dynamic library to thermopack/installed and thermopack/addon/pycThermopack/thermopack.

To configure and install the python-wrapper, run

python addon/pycThermopack/map_platform_specifics.py
pip install addon/pycThermopack/

Note: If your thermopack dynamic library is called libthermopack.dll, and not thermopack.dll, you will instead need to run

python addon/pycThermopack/map_platform_specifics.py --ifort=True
pip install addon/pycThermopack/

Legacy build system (without CMake)

Linux setup

The Thermopack source code is downloaded by cloning the library to your local computer. The following commands assume that you have a local installation of Git, gfortran and Python 3 with pip. To compile using Intel FORTRAN, use make optim_ifort.

# Fetch and compile
git clone https://github.com/thermotools/thermopack.git
cd thermopack
make optim

# Prepare and install pycThermopack, aka "thermopack"
# Remark: On some systems, Python 3 is installed as python, not python3. If so,
# you can replace "python3" with "python" and perhaps also "pip3" with "pip" in
# the below.
cd addon/pycThermopack
python3 makescript.py optim
pip3 install --user .

If you are working actively with the Thermopack code, either the Fortran backend or the Python frontend, then it may be useful to install in editable mode (aka develop mode). This will install a link to the develop files instead of copying the files when installing. This can be done with the -e option, i.e.:

pip3 install -e --user .

See also addon/pycThermopack/README.md for more details on pycThermopack.

MacOS setup

The easiest way to get started is via Homebrew. After following the instructions on their website to set it up, install gcc and make. Open a terminal (e.g. the default Terminal.app), and type:

brew install gcc make

Then follow the Linux instructions above (you may need to replace make with gmake). Some additional packages like git and python can also be installed via Homebrew before you start, but if you use a recent version of MacOS (e.g. Catalina), then the versions installed by default should be sufficient.

Windows setup

Download and compile LAPACK and BLAS libraries (you will need CMake and a working compiler).

To be compatible with the current settings, you need to compile using Intel Fortran with Visual Studio, and configure as follows:

- Fortran/Data/Default Real KIND = 8
- Fortran/External Procedures/Calling Convention = cref
- Fortran/External Procedures/Name Case Interpretation = lowercase
- Fortran/External Procedures/String Length Argument Parsing = After All Arguments
- Fortran/External Procedures/Append Underscore to External Names = Yes
- Fortran/Floating Point/Floating Point Model = precise

Copy LAPACK and BLAS libraries to the paths:

  • thermopack\lapack\lib\Debug
  • thermopack\lapack\lib\Release

Open thermopack\MSVStudio\thermopack.sln using Visual Studio, and compile the wanted configuration.

See addon/pycThermopack/README.md for how to install pycThermopack.

MSYS2/Mingw-W64 setup

Thermopack can also be compiled using gfortran in the MSYS2 environment. Download MSYS2 from https://www.msys2.org, and install and update the package system following the instructions given. Avoid having spaces in the MSYS2 installation directory path, as the Makefile might not work. Having a working MSYS2 installation, thermopack can be compiled after installing the following packages:

pacman -S git
pacman -S mingw-w64-x86_64-gcc-fortran
pacman -S mingw-w64-x86_64-openblas
pacman -S mingw-w64-x86_64-make
pacman -S mingw-w64-x86_64-dlfcn

Open the MSYS2 MinGW 64-bit application, and enter the following in the terminal:

git clone https://github.com/thermotools/thermopack.git
cd thermopack
mingw32-make.exe optim

See addon/pycThermopack/README.md for how to install pycThermopack for the MSYS2 environment.

Docker setup

See addon/docker/README.md for available Dockerfiles to run Thermopack with docker.

Getting Started - Python

Getting started - Python

This is a short introduction to thermopack. Once you've gotten started, we recommend a look at the Examples in the GitHub repo. Comprehensive documentation for the methods available through the python interface can also be found in the doc page for the thermo class.. For more advanced users, a look at the more advanced page may also be useful.

Note: This guide applies to the most recent version of ThermoPack og GitHub. For guides applicable to versions found on PyPI, find the appropriate version in the sidebar on the ThermoPack homepage.

Equations of State (EoS's) in ThermoPack are classes. To do calculations for a given mixture an EoS object must first be initialized for that mixture, as demonstrated in the Initializing an EoS section. Then, a wide variety of thermodynamic computations can be done, as demonstrated in the remaining sections.

Contents

Initialising an equation of state

An overview of available equations of state can be found here.

An EoS is initialized by passing in the fluid identifiers of the mixture, for example

from thermopack.saftvrmie import saftvrmie
eos = saftvrmie('C1,CO2')

will initialize a SAFT-VR Mie EoS for a mixture of methane and CO2. The complete list of component identifiers is in the Fluid identifiers list. PC-SAFT, SAFT-VRQ Mie and Lee-Kesler EoS are initialized in the same way, as

from thermopack import saftvrmie, saftvrqmie, pcsaft, lee_kesler
svrm = saftvrmie.saftvrmie('AR,KR') # SAFT-VR Mie EoS for Ar/Kr mixture
svrqm = saftvrqmie.saftvrqmie('HE') # SAFT-VRQ Mie EoS for pure He
pcs = pcsaft.pcsaft('BENZENE,NC6,NC12') # PC-SAFT EoS for ternary benzene/hexane/dodecane mixture
lk = lee_kesler.lee_kesler('N2,O2') # Lee-Kesler EoS for nitrogen/oxygen mixture

For PC-SAFT, both the simplified PC-SAFT (SPC-SAFT) and Polar PC-SAFT (PCP-SAFT) are available

from thermopack.pcsaft import SPC_SAFT, PCP_SAFT
spcs = SPC_SAFT('NC6,NC12') # Simplified PC-SAFT
pcps = PCP_SAFT('H2O,MEOH') # Polar PC-SAFT

The cubic equations of state are found in the cubic module. Available cubic EoS's and more information on the individual cubics, mixing rules, etc. can be found on the cubic page.

from thermopack.cubic import SoaveRedlichKwong, RedlichKwong, PengRobinson, PengRobinson78
from thermopack.cubic import SchmidtWensel, PatelTeja, VanDerWaals
srk = SoaveRedlichKwong('NH3,C2') # SRK EoS for ammonia/ethane mixture
rk = RedlichKwong('NC6,CO2,NC12') # Redlich-Kwong EoS
pr = PengRobinson('IC4,NC10') # PR EoS for isobutane/decane mixture
pr78 = PengRobinson78('N2,O2,CO2') # # PR-78 EoS for isobutane/decane mixture
vdw = VanDerWaals('C1,C2,C3,N2,O2') # VdW EoS for methane/ethane/propane/nitrogen/oxygen mixture
sw = SchmidtWensel('R11,R12') # Schmidt-Wensel EoS for FCl3C/F2Cl2C mixture
pt = PatelTeja('PRLN') # Patel-Teja EoS for pure propylene

In addition to these, the Translated-Consisten Peng-Robinson is available as

from thermopack.tcPR import tcPR
tcpr = tcPR('F6S,SO2') # Translated-Consistent PR EoS for SF6/SO2 mixture

For more fine-tuned control of the cubic EoS, the parent class cubic can be initialised directly, to explicitly set mixing rules, alpha-correlation etc.

Cubic-plus association EoS's are available for the SRK and PR EoS through the cpa module as

from thermopack.cpa import SRK_CPA, PR_CPA
srk_cpa = SRK_CPA('H2O,ETOH,PROP1OL') # SRK-CPA EoS for water/ethanol/propanol mixture

Several multiparameter EoS's can interfaced through the multiparameter.multiparam class. The available multiparameter EoS's are NIST-MEOS, MBWR16 and MBWR32. These are initialized as

from thermopack.multiparameter import multiparam
nist = multiparam('C3', 'NIST_MEOS') # NIST-MEOS EoS for propane
mbwr19 = multiparam('C1', 'MBWR19') # MBWR19 EoS for methane
mbwr32 = multiparam('C2', 'MBWR32') # MBWR32 EoS for ethane

please note that not all fluids are supported for multiparameter equations of state, depending on what parameters are available in the fluid database.

Finally, the Extended-corresponding state EoS is available through the extended_csp.ext_csp class as

from thermopack.extended_csp import ext_csp
eos = ext_csp('C1,C2,C3,NC4', sh_eos='SRK', sh_alpha='Classic',
              sh_mixing='vdW', ref_eos='NIST_MEOS', ref_comp='C3')

For more information on the extended-csp EoS please see the Examples and the memo.

Doing calculations

Now that we have an EoS initialized we can start computing stuff. The primary source on how to use individual methods in thermopack are the specific documentation of the thermo class. Here, a small subset of the functionality is demonstrated.

Note that all input is in SI units (moles/kelvin/pascal/cubic meters/joule)

pVT-properties

Specific volume, given temperature, pressure and composition is computed as

from thermopack.saftvrmie import saftvrmie
eos = saftvrmie('NC6,NC10') # Hexane/decane mixture
T = 300 # Kelvin
p = 1e5 # Pascal
x = [0.2, 0.8] # Molar composition
vg, = eos.specific_volume(T, p, x, eos.VAPPH) # Molar volume of gas phase (NB: Notice the comma)
vl, = eos.specific_volume(T, p, x, eos.LIQPH) # Molar volume of liquid phase (NB: Notice the comma)

where eos.VAPPH and eos.LIQPH are phase flags used to identify different phases. The commas are necessary because all output from thermopack methods are as tuples.

Similarly, pressure, internal energy, enthalpy, entropy, etc. and associated differentials can be computed via the methods chemical_potential_tv(T, V, n), internal_energy_tv(T, V, n), enthalpy_tv(T, V, n), helmholtz_tv(T, V, n), entropy_tv(T, V, n). For a full overview of the available property calculations see the TV-property interfaces and the Tp-property interfaces of the thermo class

Differentials

If we want volume differentials, we use the same method, but set the flags to calculate differentials to True:

# Continued 
vg, dvdp = eos.specific_volume(T, p, x, eos.VAPPH, dvdp=True) # Vapour phase molar volume and pressure differential
vl, dvdT = eos.specific_volume(T, p, x, eos.LIQPH, dvdt=True) # Liquid phase molar volume and temperature differential
_, dvdn = eos.specific_volume(T, p, x, eos.LIQPH, dvdn=True) # Liquid phase partial molar volumes

Differentials can be computed as functions of $(T, V, n)$ or as functions of $(T, p, n)$. For an overview of the different methods, see Advanced usage: Different property interfaces. A short example is given here as:

# Continued
n_tot = 15 # Total number of moles
n = n_tot * x
H, dHdn_TV = eos.enthalpy_tv(T, vg, n, dhdn=True) # Compute enthalpy and derivative of enthalpy wrt. mole numbers at constant (T, V)
h_vap, dhvap_dn_Tp = eos.enthalpy(T, p, x, eos.VAPPH, dhdn=True) # Compute molar vapour phase enthalpy and derivative of molar vapour phase enthalpy wrt. mole numbers at constant (T, p)
h_liq, dliq_dn_Tp = eos.enthalpy(T, p, x, eos.LIQPH, dhdn=True) # Compute molar liquid phase enthalpy and derivative of molar liquid phase enthalpy wrt. mole numbers at constant (T, p)
H, dHdn_Tp = eos.enthalpy_tvp(T, vg, n, dhdn=True) # Compute enthalpy and derivative of enthalpy wrt. mole numbers at constant (T, p)

Please note that heat capacities are not available directly, but must be computed as derivatives of enthalpy and internal energy, as

from thermopack.cubic import cubic
eos = cubic('C1,C3,NC6', 'SRK') # SRK EoS for a mixture of methane, propane and n-hexane

T = 300 # Kelvin
p = 1e5 # Pascal
x = [0.2, 0.1, 0.7] # Molar composition
_, Cp_vap = eos.enthalpy(T, p, x, eos.VAPPH, dhdt=True) # Vapour phase heat capacity at constant pressure, computed as (dH/dT)_{p,n}
_, Cp_liq = eos.enthalpy(T, p, x, eos.LIQPH, dhdt=True) # Liquid phase heat capacity at constant pressure, computed as (dH/dT)_{p,n}

vg, = eos.specific_volume(T, p, x, eos.VAPPH) # Computing vapour phase specific volume
vl, = eos.specific_volume(T, p, x, eos.LIQPH) # Liquid phase specific volume

_, Cv_vap = eos.internal_energy_tv(T, vg, x, dedt=True) # Vapour phase heat capacity at constant volume, computed as (dU/dT)_{V,n}
_, Cv_liq = eos.internal_energy_tv(T, vl, x, dedt=True) # Liquid phase heat capacity at constant volume, computed as (dU/dT)_{V,n}

Phase diagrams and Equilibria

As with other calculations, the primary source on how available methods for flash- and equilibria calculations and how to use them is the documentation of the thermo class.. Here we give a short introduction, for more extensive examples see the pyExamples directory.

Flash calculations

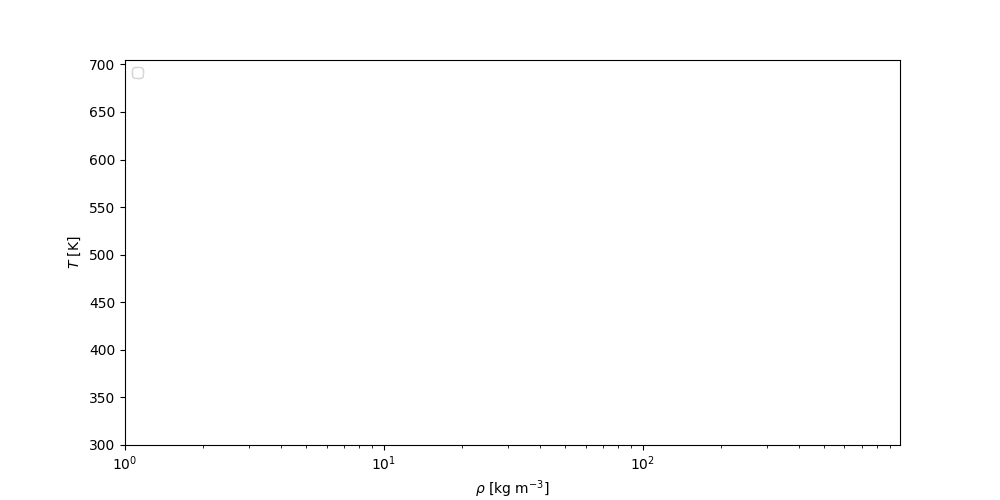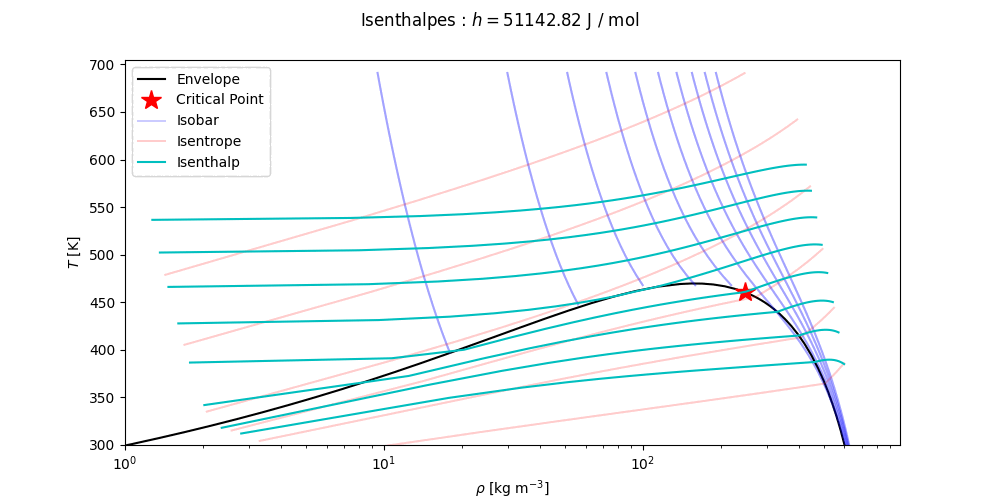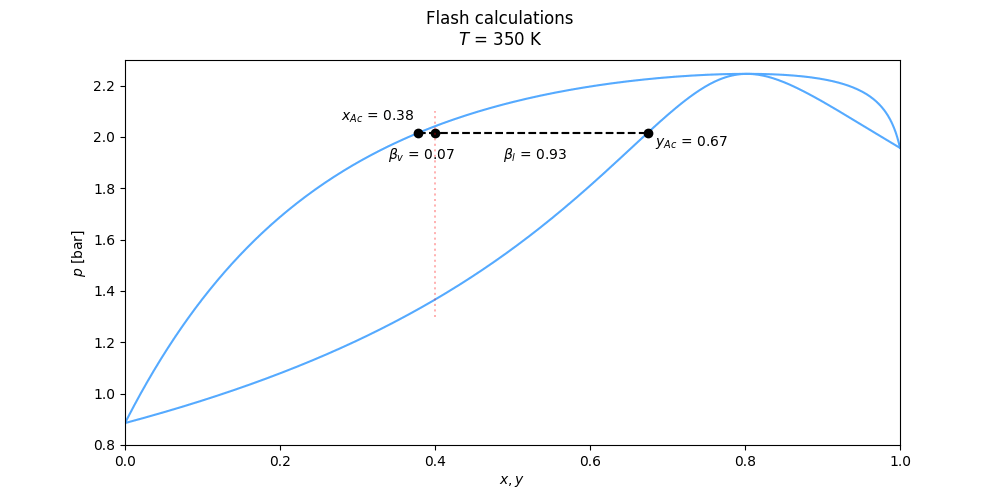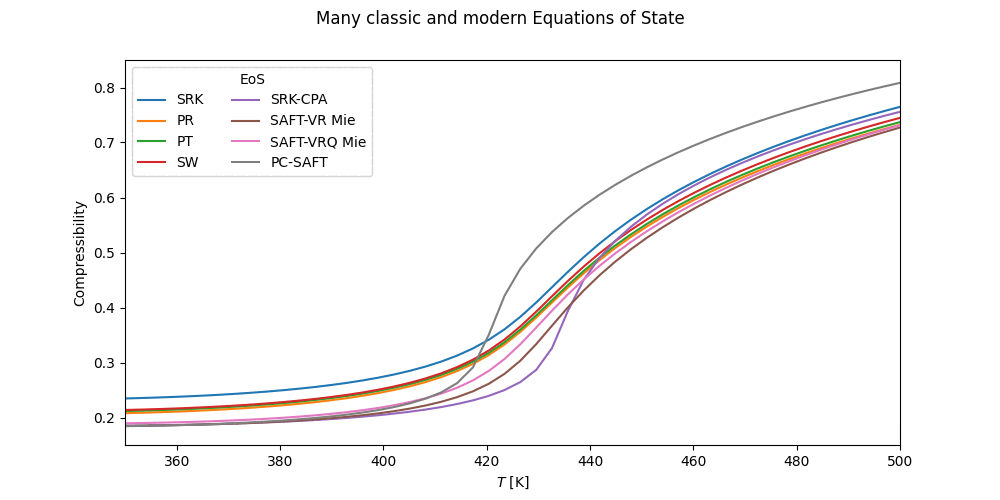
Flash calculations of several kinds are handled by the methods twophase_tpflash(), twophase_psflash(), twophase_phflash() and twophase_uvflash().

See the Flash interfaces in the documentation of the thermo class for the specifics on the different flash routines.

An example calculation using twophase_tpflash() may be done as

from thermopack.saftvrqmie import saftvrqmie
# SAFT-VRQ Mie for Hydrogen/Helium/Neon mixture 
eos = saftvrqmie('H2,HE,NE', minimum_temperature=20) # NB: Set minimum temperature low enough when working at very low temperatures
T = 35 # Kelvin
p = 3e6 # Pascal (30 bar)
z = [0.1, 0.25, 0.65] # Molar composition
flsh = eos.two_phase_tpflash(T, p, z) # flsh is a FlashResult object
print(flsh)
### Output: ###
# FlashResult object for Tp-flash
# Containing the attributes (description, name, value):
#   	Flash type                     flash_type : Tp  
#   	Total composition              z     : [0.1, 0.25, 0.65]  
#   	Temperature [K]                T     : 35  
#   	pressure [Pa]                  p     : 3000000.0  
#   	Liquid phase composition       x     : [0.05407302 0.03859287 0.90733411]  
#   	Vapour phase composition       y     : [0.14642524 0.46370066 0.3898741 ]  
#   	Vapour fraction                betaV : 0.497302408174766  
#   	Liquid fraction                betaL : 0.5026975918252341  
#   	Phase indentifier index        phase : 0

the result of the flash is accessed from the attributes of the FlashResult object, found in utils.py, as

# Continued
x = flsh.x # Liquid composition
y = flsh.y # Vapour composition
betaL = flsh.betaL # Liquid fraction
# ... etc

The FlashResult object returned by the different flash routines all contain the same attributes.

Phase envelopes

ThermoPack has interfaces to trace (T,p)-, (T,v)- and (p,x,y)-phase envelopes. For the full documentation, see the docs of the thermo class. For more comprehensive examples, see the Examples.

Tp- and Tv- phase envelopes

Phase envelopes can be generated directly with the method get_envelope_twophase() as

# Continued
T, p = eos.get_envelope_twophase(1e5, x) # arrays of temperature and pressure for phase envelope, starting at 1 bar.
plt.plot(p, T) # Tp-projection of phase envelope

T, p, v = eos.get_envelope_twophase(1e5, x, calc_v=True) # Also return the specific volume at each point along the phase envelope
plt.plot(1 / v, T) # rho-T projection of the phase envelope

pxy- and txy- phase envelopes

To compute pxy-type phase envelopes, we use the get_binary_pxy() method. This method returns a XYDiagram struct, which holds the composition and pressure / temperature of each equilibrium phase.

The XYDiagram struct has the attributes lle, l1ve and l2ve, where

  • lle holds the composition and pressure / temperature of the Liquid 1 - Liquid 2 equilibria
    • lle.x1 is the composition of Liquid 1 (mole fraction of species 1)
    • lle.x2 is the composition of Liquid 2 (mole fraction of species 1)
    • lle.p / lle.T is the pressure / temperature along the phase boundary
  • l1ve holds the composition and pressure / temperature of the Liquid 1 - Vapour equilibria
    • l1ve.x is the composition of Liquid 1 (mole fraction of species 1)
    • l1ve.y is the composition of the vapour (mole fraction of species 1)
    • l1ve.p / l1ve.T is the pressure / temperature along the phase boundary
  • l2ve holds the composition and pressure / temperature of the Liquid 2 - Vapour equilibria
    • l2ve.x is the composition of Liquid 2 (mole fraction of species 1)
    • l2ve.y is the composition of the vapour (mole fraction of species 1)
    • l2ve.p / l2ve.T is the pressure / temperature along the phase boundary

We get the phase diagram as

from thermopack.cpa import SRK_CPA

eos = SRK_CPA('NC6,H2O')  # CPA-SRK eos for Hexane/water mixture
T = 350
pxy = eos.get_binary_pxy(T)  # Returns a XYDiagram struct
print(pxy)
# Result:
# XYDiagram object with attributes (name : description)
# lle  : Liquid 1 - Liquid 2 Equilibrium
# 	PxyEquilibrium object with attributes (description, name, value)
# 		Type of equilibrium                   type : lle
# 		Liquid 1 mole fraction, species 1     x1   : [4.278e-07 ... 4.145e-07], len(x1) = 457
# 		Liquid 2 mole fraction, species 1     x2   : [9.969e-01 ... 9.974e-01], len(x2) = 457
# 		Pressure                              p    : [1.648e+05 ... 1.500e+07], len(p) = 457
# 	
# l1ve : Liquid 1 - Vapour Equilibrium
# 	PxyEquilibrium object with attributes (description, name, value)
# 		Type of equilibrium                   type : lve
# 		Liquid mole fraction, species 1       x    : [4.278e-07 ... 2.197e-07], len(x) = 66
# 		Vapour mole fraction, species 1       y    : [7.880e-01 ... 6.461e-01], len(y) = 66
# 		Pressure                              p    : [1.648e+05 ... 1.000e+05], len(p) = 66
# 	
# l2ve : Liquid 2 - Vapour Equilibrium 
# 	PxyEquilibrium object with attributes (description, name, value)
# 		Type of equilibrium                   type : lve
# 		Liquid mole fraction, species 1       x    : [9.969e-01 ... 1.000e+00], len(x) = 100
# 		Vapour mole fraction, species 1       y    : [7.880e-01 ... 1.000e+00], len(y) = 100
# 		Pressure                              p    : [1.648e+05 ... 1.289e+05], len(p) = 100

For ease of use, the XYDiagram struct is iterable, such that we can unpack it efficiently as

lle, l1ve, l2ve = pxy

Now, we can plot the phase diagram as

# Continued
import matplotlib.pyplot as plt

# Liquid-liquid phase boundaries
# pxy.lle holds the composition and pressure of the liquid phases
plt.plot(pxy.lle.x1, pxy.lle.p, label='Liquid 1 composition') # lle.x1 is the mole fraction of component 1 (NC12) in Liquid 1 along the phase boundary
plt.plot(pxy.lle.x2, pxy.lle.p, label='Liquid 2 composition') # lle.x2 is the mole fraction of component 1 (NC12) in Liquid 2 along the phase boundary

# Liquid 1-vapour phase boundaries
# pxy.l2ve holds composition and pressure along the Liquid 1 - Vapour phase boundary
plt.plot(pxy.l1ve.x, pxy.l1ve.p, label='Liquid 1 bubble line') # l1ve.x is the mole fraction of component 1 (NC12) in Liquid 1 along the Liquid 1 - Vapour phase boundary
plt.plot(pxy.l1ve.y, pxy.l1ve.p, label='Liquid 1 dew line') # l1ve.y is the mole fraction of component 1 (NC12) in the Vapour phase along the Liquid 1 - Vapour phase boundary

# Liquid 2-vapour phase boundaries
# L2VE[2] is the pressure along the Liquid 2 - Vapour phase boundary
plt.plot(pxy.l2ve.x, pxy.l2ve.p, label='Liquid 2 bubble line') # l2ve.x is the mole fraction of component 1 (NC12) in Liquid 2 along the Liquid 2 - Vapour phase boundary
plt.plot(pxy.l2ve.y, pxy.l2ve.p, label='Liquid 2 dew line') # l2ve.y is the mole fraction of component 1 (NC12) in the Vapour phase along the Liquid 2 - Vapour phase boundary

plt.ylabel('Pressure [Pa]') # The third element in each tuple is the pressure along the phase boundary
plt.xlabel('Molar composition')

The method get_binary_txy works in the same way, only replacing the p attribute with T, such that we can compute

p = 1e5
lle, l1ve, l2ve = eos.get_binary_txy(p) # Unpacking the XYDiagram 

# Liquid-liquid phase boundaries
# l1ve holds the composition and pressure of Liquid 1 and Vapour along the phase boundary
plt.plot(l1ve.x, l1ve.T, label='Liquid 1 composition') # l1ve.x is the mole fraction of component 1 (NC12) in Liquid 1 along the phase boundary
plt.plot(l1ve.y, l1ve.T, label='Vapour composition') # l1ve.y is the mole fraction of component 1 (NC12) in Vapour along the phase boundary

# ... etc ...

If an equilibrium is not found, for example there is only one vapour-liquid equilibria, and no liquid-liquid equilibria, the arrays corresponding to the non-existent equilibria are empty, i.e.

T = 300
pxy = get_binary_pxy(T) # Some mixture that has only one vapour - liquid equilibria at 300 K
print(len(pxy.lle.x1) == 0) # True
print(len(pxy.lle.x2) == 0) # True
print(len(pxy.lle.p) == 0) # True
print(len(pxy.l1ve.x) == 0) # False
print(len(pxy.l1ve.y) == 0) # False
print(len(pxy.l1ve.p) == 0) # False
print(len(pxy.l2ve.x) == 0) # True
print(len(pxy.l2ve.y) == 0) # True
print(len(pxy.l2ve.p) == 0) # True

Dew- and bubble points

We can also compute the bubble-temperature, pressure etc. directly using the methods bubble_temperature(p, z), bubble_pressure(T, z), dew_temperature(p, z) and dew_pressure(T, z), where z is the composition of the mixture, as

eos = cubic('CO2,C1', 'SRK')
x = [0.5, 0.5] # Total composition of the mixture
p_dew, y_dew = eos.dew_pressure(250, x) # Calculates dew pressure and dew composition at 250 K
T_dew, y_dew = eos.dew_temperature(1e5, x) # Calculates dew temperature and dew composition at 1 bar
p_bub, x_bub = eos.bubble_pressure(230, x) # Calculates bubble pressure and bubble composition at 230 K
T_bub, x_bub = eos.bubble_temperature(1e5, x) # Calculates bubble temperature and bubble composition at 1 bar

Isolines

Various isolines can be computed using the methods get_isotherm, get_isobar, get_isentrope and get_isenthalp. In the following code snippet, the default values of the keyword arguments are indicated.

from thermopack.pcsaft import pcsaft
eos = pcsaft('NC6,NC12')
x = [0.2, 0.8]

# Calculate pressure, specific volume, specific entropy and specific enthalpy along the isotherm at 300 K
# from p = minimum_pressure to p = maximum_pressure. Compute at most nmax points.
p_iso_T, v_iso_T, s_iso_T, h_iso_T = eos.get_isotherm(300, x, minimum_pressure=1e5, maximum_pressure=1.5e7, nmax=100)

# Calculate temperature, specific volume, specific entropy and specific enthalpy along the isobar at 1 bar
# from T = minimum_temperature to T = maximum_temperature. Compute at most nmax points.
T_iso_p, v_iso_p, s_iso_p, h_iso_p = eos.get_isobar(1e5, x, minimum_temperature=200, maximum_temperature=500, nmax=100)

# Calculate temperature, pressure, specific volume and specific entropy along the isenthalp at 1 kJ / mol
# Start at the upper of (minimum_pressure, minimum_temperature)
# End at the lower of (maximum_pressure, maximum_temperature)
T_iso_h, p_iso_h, v_iso_h, s_iso_h = eos.get_isenthalp(1e3, x, minimum_pressure=1e5, maximum_pressure=1.5e7,
                                                            minimum_temperature=200, maximum_temperature=500,
                                                            nmax=100)

# Calculate temperature, pressure, specific volume and specific enthalpy along the isentrope at 5 J / mol K
# Start at the upper of (minimum_pressure, minimum_temperature)
# End at the lower of (maximum_pressure, maximum_temperature)
T_iso_s, p_iso_s, v_iso_s, h_iso_s = eos.get_isentrope(5, x, minimum_pressure=1e5, maximum_pressure=1.5e7,
                                                            minimum_temperature=200, maximum_temperature=500,
                                                            nmax=100)

Critical point

Thermopack has a critical point solver, which is called as

eos = saftvrqmie('HE,NE') # Use FH-corrected Mie potentials for Helium calculations!
n = [5, 10]
Tc, Vc, pc = eos.critical(n) # Compute the critical temperature, pressure and volume given mole numbers
vc = Vc / sum(n) # Critical specific volume computed from critical volume and mole numbers.

The solver accepts initial guesses for the critical values through the kwargs temp, and v. The error tolerance can be set via the tol kwarg (default is tol=1e-7).

More advanced usage

Interaction parameters

In thermopack we're able to both set and get a wide array of coefficients and parameters depending on the models we are utilizing.

Cubic equations of state

Setting and getting the attractive energy interaction parameter $k_{ij}$ and co-volume interaction parameter $l_{ij}$

Starting with the attractive energy interaction parameter (kij). The parameter can be set using the function set_kij after initialising the equation and state. The function requires that you first write in the number of the components and subsequently the new interaction parameter i.e. (component number 1, component number 2, new kij value). If we're curious as to what parameter the EOS is already using we can see this by using the function get_kij which returns the value as a float given the component numbers as input i.e. (component number 1, component number 2).

cs = cubic('CO2,N2',"SRK","Classic","Classic")
#We set the interaction parameter to be -0.032
cs.set_kij(1,2,-0.032)
#We want to see what the interaction parameter is which returns that kij = -0.032
kij = cs.get_kij(1,2)

The procedure for setting and getting co-volume interaction parameters is analogous to the getting and setting of attractive energy parameters. Simply use the functions set_lij and get_lij instead.

#We set the parameter to be -0.032
cs.set_lij(1,2,-0.032)
#We want to see what the parameter is which returns that lij = -0.032
lij = cs.get_lij(1,2)

Tuning Cubics

Cubic Equations of state implemented in ThermoPack can be accessed through the generic cubic class. This class also offers a variety of methods to tune the alpha-function, mixing rules etc. See the documentation for the cubic class for more information.

The different property interfaces (TV-) (Tp-) and (TVp-)

Property calculations in ThermoPack can be done either through the TV-interfaces, the Tp-interfaces or the TVp-interfaces.

The difference between the TV- and Tp- interface is only what variables the properties are computed as functions of, and what variables are held constant in the derivatives. TV-interface methods compute properties as functions of $(T, V, n)$, while Tp-interface methods compute properties as functions of $(T, p, n)$.

The TVp-interface methods on the other hand take $(T, V, n)$ as arguments, and evaluate derivatives as functions of $(T, p, n)$. To demonstrate with an example:

import numpy as np
from thermopack.cubic import cubic

eos = cubic('O2,N2', 'PR') # PR EoS for O2/N2 mixture

T = 300 # Kelvin
p = 1e5 # Pascal
x = np.array([0.21, 0.79]) # Molar composition (of air)
n_tot = 10 # Total number of moles
n = n_tot * x # Vector of mole numbers

v, = eos.specific_volume(T, p, x, eos.VAPPH) # Compute specific volume of vapour phase
V = v * n_tot # Total volume


# Computing the TOTAL Enthalpy (J), given (T, V, n)
# The differentials are computed for H = H(T, V, n), with 
# "subscripts" indicating the variables held constant
H_tvn, dHdT_Vn, dHdn_TV = eos.enthalpy_tv(T, V, n, dhdt=True, dhdn=True) 

# Computing the SPECIFIC VAPOUR phase enthalpy (J / mol), given (T, p, n) 
# The differentials are computed for h_vap = h_vap(T, p, n), with the 
# "subscripts" indicating the variables held constant
h_vap_tpn, dh_vap_dt_pn, dh_vap_dn_Tp = eos.enthalpy(T, p, n, eos.VAPPH, dhdt=True, dhdn=True)

# Computing the SPECIFIC LIQUID phase enthalpy (J / mol), given (T, p, n) 
# The differentials are computed for h_liq = h_liq(T, p, n), with the 
# "subscripts" indicating the variables held constant
h_liq_tpn, dh_liq_dt_pn, dh_liq_dn_Tp = eos.enthalpy(T, p, n, eos.LIQPH, dhdt=True, dhdn=True)

# Computing the TOTAL Enthalpy (J), given (T, V, n)
# NOTE : The differentials are computed for H = H(T, p, n)
#        NOT for H = H(T, V, n)
H_tpn, dHdt_pn, dHdn_Tp = eos.enthalpy_tvp(T, V, n, dhdt=True, dhdn=True)

Besides enthalpy_tvp, there are currently available TVp-interfaces for entropy_tvp and thermo_tvp (logarithm of fugacity coefficients).

Adding new fluids

The fluid database consists of a set of .json-files in the fluids directory. These files are are used to auto-generate the FORTRAN-files compdatadb.f90 and saftvrmie_datadb.f90 by running the respective python scripts compdata.py and saftvrmie.py found in the directory addon/pyUtils/datadb/. The files are generated in the current working directory and must be copied to the src-directory before recompiling ThermoPack to make the fluids available.

A <fluid\>.json file must contain a minimal set of data to be valid. This includes the critical point, accentric factor, mole weight and ideal gas heat capacity.

Ideal gas heat capacity

Several different correlations for the heat capacity are available, selected by the "correlation"-key in the "ideal-heat-capacity-1" field of the fluid files. These are summarized in the table below.

Ideal gas heat capacity correlations, and the corresponding keys used in the fluid-database.
Key Correlation Equation Unit
1 Sherwood, Reid & Prausnitz(a) $A + BT + CT^2 + DT^3$ $\text{cal mol}^{-1} \rm{K}^{-1}$
2 API-Project 44 -
3 Hypothetic components - -
4 Sherwood, Reid & Prausnitz(b) $A + BT + CT^2 + DT^3$ $\rm{J mol}^{-1} \rm{K}^{-1}$
5 Ici (Krister Strøm) $A + BT + CT^2 + DT^3 + ET^{-2}$ $\rm{J g}^{-1} \rm{K}^{-1}$
6 Chen, Bender (Petter Nekså) $A + BT + CT^2 + DT^3 + ET^4$ $\rm{J g}^{-1} \rm{K}^{-1}$
7 Aiche, Daubert & Danner(c) $A + B [ (C / T) \sinh(C/T) ]^2 + D [ (E / T) \cosh(E / T) ]^2$ $\rm{J kmol}^{-1} \rm{K}^{-1}$
8 Poling, Prausnitz & O’Connel(d) $R ( A + BT + CT^2 + DT^3 + ET^4 )$ $\rm{J mol}^{-1} \rm{K}^{-1}$
9 Linear function and fraction $A + BT + C(T + D)^{-1}$ $\rm{J mol}^{-1} \rm{K}^{-1}$
10 Leachman & Valenta for H2 - -
11 Use TREND model - -
12 Shomate equation $^{(*)}$ $A + B T_{\rm{s}} + C T_{\rm{s}}^2 + D T_{\rm{s}}^3 + E T_{\rm{s}}^{-2}$ $\rm{J mol}^{-1} \rm{K}^{-1}$
13 Einstein equation sum $R (A + \sum_i B_i (C_i / T)^2 \exp[C_i / T] / (\exp[C_i / T] - 1)^2)$ $\rm{J mol}^{-1} \rm{K}^{-1}$

(a)3rd ed.(c)DIPPR-database

(b)4th ed.(d)5th ed.

${(*)}$ Note:$T_{\rm{s}}= 10^{-3} T$

Melting and sublimation curve correlations

$T_{\rm{reducing}} (K), p_{\rm{reducing}} (Pa), \mathbf{a}, \mathbf{c}, n, n_1, n_2$ and $n_3$ are read from the <fluid\>.json file, while $n_4 = n-n_1- n_2-n_3$. Currently a maximum of 6 parameters can be given, $n \leq 6$. The correlation type is defined by a four character string with the format XX-X, where ML-X and SL-X are the default melting curve ($\sigma_{\rm{melt}}$) and sublimation curve ($\sigma_{\rm{sub}}$) correlations, respectively. See the Methane.json file for an working example of both the melting_curve and sublimation_curve parameters.

The reduced temperature used in the correlations is defined as

$$ \tau = \frac{T}{T_{\rm{reducing}}}. $$

The last character in the correlation string defines how the reducing pressure combines with $\sigma$ to give the melting/sublimation pressure,

$$ p(\sigma) = p_{\rm{reducing}} \times \begin{cases} \sigma & \text{correlation is XX-1} \\\ \exp(\sigma) & \text{correlation is XX-2}\\\ \exp(\frac{\sigma}{\tau}) & \text{correlation is XX-3} \end{cases} $$

For the melting curve calculation $\sigma$ is calculated from

$$ \sigma_{\rm{melt}} = \sum_{i=1}^{n_1} a_i \tau^{c_i} + \sum_{j=1}^{n_2} a_j (\tau-1)^{c_j} + \sum_{k=1}^{n_3} a_k (\ln \tau)^{c_k} + \sum_{l=1}^{n_4} a_l (\tau^{c_l} - 1) $$

For the sublimation curve calculation $\sigma$ is calculated from

$$ \sigma_{\rm{sub}} = \sum_{i=1}^{n_1} a_i \tau^{c_i} + \sum_{j=1}^{n_2} a_j (1-\tau)^{c_j} + \sum_{k=1}^{n_3} a_k (\ln \tau)^{c_k} + \sum_{l=1}^{n_4} a_l (\tau^{c_l} - 1) $$

The melting/sublimation curves can be scaled to match the saturation pressure at the triple temperature, $p_{\rm{sat}}(T_{\rm{triple}})$. The scaled pressure, $\tilde{p}(\sigma)$, is then calculated as

$$ \tilde{p}(\sigma) = \frac{p_{\rm{sat}}(T_{\rm{triple}}) }{p(\sigma(T_{\rm{triple}}))} p(\sigma)$$

Component identifiers

Fluid name to fluid identifier mapping

 

In order to specify fluids in Thermopack you need to use fluid identifiers as shown in the table below. The 'SAFT-VR', 'PC-SAFT' and 'CPA' columns indicate which fluids SAFT-EoS and CPA parameters are available for.

  You may have to scroll right to view the whole table.

Fluid name CAS Number Fluid identifyer SAFT-VR PC-SAFT CPA
1,1,1,2-Tetrafluoroethane 811-97-2 R134a
1,1,1-Trifluoroethane 420-46-2 R143a
1,1-Difluoroethane 75-37-6 R152a
1,1-Difluoroethylene 75-38-7 R1132a
1,2-Dichlorotetrafluoroethane 76-14-2 R114
1,3-Butadiene 106-99-0 13BD
1-Butanol 71-36-3 BUT1OL ✔ ✔
1-Chloro-1,1,2,2-tetrafluoroethane 354-25-6 R124a
1-Chloro-1,1-difluoroethane 75-68-3 R142b
1-Hexanol 111-27-3 HEX1OL ✔ ✔
1-Pentanol 71-41-0 PENT1OL ✔ ✔
1-Propanol 71-23-8 PROP1OL ✔ ✔
2,3,3,3-Tetrafluoropropene 754-12-1 R1234yf
2-Chloro-1,1,1,2-tetrafluoroethane 2837-89-0 R124
2-Methylhexane 591-76-4 2MHX
3-Methylpentane 96-14-0 3MP
Acetone 67-64-1 ACETONE ✔
Acetylene 74-86-2 ACETYLENE ✔
Ammonia 7664-41-7 NH3 ✔ ✔ ✔
Argon 7440-37-1 AR ✔ ✔
Benzene 71-43-2 BENZENE ✔
Butanal 123-72-8 BUTANAL ✔
Carbon dioxide 124-38-9 CO2 ✔ ✔ ✔
Carbon monoxide 630-08-0 CO
Carbon tetrafluoride 75-73-0 R14
Chlorine 7782-50-5 CL2 ✔
Chlorodifluoromethane 75-45-6 R22
Chloropentafluoroethane 76-15-3 R115
Chlorotrifluoromethane 75-72-9 R13
Chlorotrifluorosilane 14049-36-6 ClF3Si
Cyclohexane 110-82-7 CYCLOHEX ✔
Cyclopropane 75-19-4 C3_1
Deuterium 7782-39-0 D2 ✔
Di-methyl ether 115-10-6 DME ✔
Di-n-hexyl ether 112-58-3 S434
Dichlorodifluoromethane 75-71-8 R12
Dichlorofluoromethane 75-43-4 R21
Difluoromethane 75-10-5 R32
Dinitrogen tetroxide 10544-72-6 N2O4
Equilibrium-hydrogen 1333-74-0 E-H2
Ethane 74-84-0 C2 ✔ ✔
Ethanol 64-17-5 ETOH ✔ ✔ ✔
Ethylbenzene 100-41-4 EBZN
Ethylene glycol 107-21-1 MEG
Ethylene 74-85-1 C2_1 ✔
Helium-4 7440-59-7 HE ✔
Hexafluoroethane 76-16-4 R116
Hydrazine 302-01-2 N2H4 ✔
Hydrogen peroxide 7722-84-1 H2O2
Hydrogen sulfide 7783-06-4 H2S ✔ ✔
Hydrogen 1333-74-0 H2 ✔
Isobutane 75-28-5 IC4 ✔
Isopentane 78-78-4 IC5 ✔
Krypton 7439-90-9 KR ✔ ✔
Lennard-jones_fluid LJF ✔
Methane 74-82-8 C1 ✔ ✔
Methanol 67-56-1 MEOH ✔ ✔ ✔
Methyl fluoride 593-53-3 R41
Methylcyclopentane 96-37-7 MTC5
Neon 7440-01-9 NE ✔
Nitric oxide 10102-43-9 NO
Nitrogen 7727-37-9 N2 ✔ ✔
Nitrous oxide 10024-97-2 N2O
Octafluoropropane 76-19-7 R218
Ortho-hydrogen 1333-74-0 O-H2 ✔
Oxygen 7782-44-7 O2 ✔ ✔
Para-hydrogen 1333-74-0 P-H2 ✔
Pentafluoroethane 354-33-6 R125
Propadiene 463-49-0 ALLENE
Propane 74-98-6 C3 ✔ ✔ ✔
Propylene 115-07-1 PRLN
Pseudo XXX PSEUDO
Sulfur dioxide 7446-09-5 SO2
Sulfur hexafluoride 2551-62-4 F6S
Tetrafluoroethylene 116-14-3 R1114
Tetrafluorohydrazine 10036-47-2 F4N2
Toluene 108-88-3 TOLU ✔
Trans-1,3,3,3-tetrafluoropropene 29118-24-9 R1234ze
Trichlorofluoromethane 75-69-4 R11
Trifluoroamine oxide 13847-65-9 F3NO
Trifluoromethane 75-46-7 R23
Water 7732-18 H2O ✔ ✔ ✔
Xenon 7440-63-3 XE ✔
m-Xylene 108-38-3 MXYL
n-Butane 106-97-8 NC4 ✔ ✔ ✔
n-Decane 124-18-5 NC10 ✔ ✔ ✔
n-Docosane 629-97-0 NC22 ✔ ✔
n-Dodecane 112-40-3 NC12 ✔
n-Eicosane 112-95-8 NC20 ✔ ✔
n-Heneicosane 629-94-7 NC21 ✔
n-Heptadecane 629-78-7 NC17 ✔
n-Heptane 142-82-5 NC7 ✔ ✔ ✔
n-Hexadecane 544-76-3 NC16 ✔
n-Hexane 110-54-3 NC6 ✔ ✔ ✔
n-Hydrogen 1333-74-0 N-H2
n-Nonadecane 629-92-5 NC19 ✔
n-Nonane 111-84-2 NC9 ✔ ✔ ✔
n-Octadecane 593-45-3 NC18 ✔
n-Octane 111-65-9 NC8 ✔ ✔ ✔
n-Pentacosane 629-99-2 NC25 ✔
n-Pentadecane 629-62-9 NC15 ✔ ✔
n-Pentan 109-66-0 NC5 ✔ ✔ ✔
n-Tetracosane 646-31-1 NC24 ✔
n-Tetradecane 629-59-4 NC14 ✔
n-Tricosane 638-67-5 NC23 ✔
n-Tridecane 629-50-5 NC13 ✔
n-Undecane 1120-21-4 NC11 ✔
o-Xylene 95-47-6 OXYL
p-Xylene 106-42-3 PXYL

About

Thermopack is a thermodynamic model library for fluid properties and PVT calculations

Resources

Readme

License

Unknown, MIT licenses found

Licenses found

Unknown
LICENSE-APACHE
MIT
LICENSE-MIT
Activity
Custom properties

Stars

54 stars

Watchers

7 watching

Forks

13 forks
Report repository

Releases 4

v2.2.4 Latest
Oct 15, 2024
+ 3 releases

Packages

No packages published

Contributors 5

Languages