-
Notifications
You must be signed in to change notification settings - Fork 153
Polígonos
Polígonos são figuras planas delimitadas por caminhos fechados (o vértice de partida é o vértice de chegada), compostos por segmentos de retas que une pontos (vértices) consecutivos. Os segmentos que unem os vértices são denominados arestas.
A maior parte dos problemas de Geometria Computacional envolvem polígonos. Embora alguns polígonos especiais (triângulos, quadriláteros) já tenham sido expostos anteriormente, a abordagem desta seção é mais geral, e pode ser aplicada a qualquer polígono com qualquer número de vértices.
A representação mais comum de um polígono é a listagem de seus vértices, sendo que as arestas ficam subentendidas (há sempre uma aresta unindo dois vértice consecutivos). Para facilitar a implementação de algumas rotinas, pode ser conveniente inserir, ao final da lista, o ponto de partida, mas é preciso tomar cuidado: ao fazer isso, o número de vértices do polígono passa a ser o número de elementos da lista subtraído de uma unidade.
// Definição da classe Point
using Polygon = vector<Point>;Esta primeira implementação é a mais compacta possível, mas requer atenção a questão do número de vértices, conforme já comentado. A implementação abaixo é mais extensa, porém evita os problemas já mencionados.
// Definição da classe Point
class Polygon {
public:
vector<Point> vertices;
int n;
// O parâmetro deve conter os n vértices do polígono
Polygon(const vector<Point>& vs) : vertices(vs), n(vs.size())
{
vertices.push_back(vertices[0]);
}
};Importante notar que ambas implementações não checam a validade do polígono no que se refere ao número de vértices: um polígono deve ter, no mínimo, três vértices.
O perímetro de um polígono pode ser calculado diretamente a partir da representação proposta, pois consiste na medida do contorno do polígono, isto é, a soma dos comprimentos de cada aresta.
// Definição da classe Point
class Polygon {
public:
// Membros e construtor
double perimeter() const
{
double p = 0;
for (int i = 0; i < n; ++i)
p += vertices[i].distance(vertices[i + 1]);
return p;
}
};Já a área de um polígono pode ser também determinada diretamente da representação dada. Ela corresponde a metade do valor absoluto do "determinante" abaixo (as aspas significam que a notação remete a um determinante, mas não é um determinante de fato, uma vez que a matriz não é quadrada).
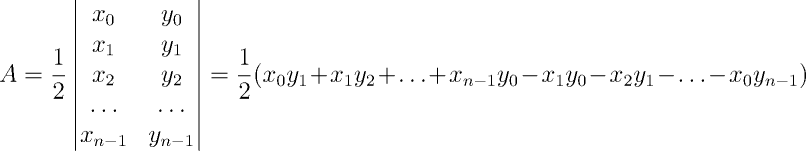
// Definição da classe Point
class Polygon {
public:
// Membros e construtor
double area() const
{
double a = 0;
for (int i = 0; i < n; ++i)
{
a += vertices[i].x * vertices[i+1].y;
a -= vertices[i+1].x * vertices[i].y;
}
return 0.5 * fabs(a);
}
};Caso o polígono seja regular (isto é, todos os lados tenham a mesma medida), a área também pode ser computada através do conhecimento do número de lados n e um dos três valores abaixo:
- comprimento de um dos lados (s);
- apótema, ou raio do círculo inscrito (r);
- raio do círculo circunscrito (R);
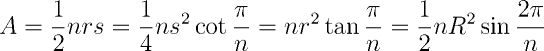
Um polígono é dito convexo se, para quaisquer dois pontos P e Q localizados no interior do polígono, o segmento de reta PQ não intercepta nenhuma das arestas do polígono. Caso contrário, o polígono é dito côncavo.
É possível determinar se um polígono é ou não convexo sem recorrer à busca completa (isto é, testar todos os possíveis pares de pontos interiores ao polígono): a rotina de orientação entre pontos e reta (discutida na seção Retas) pode ser utilizada para tal fim. Basta checar se, para quaisquer três pontos consecutivos do polígono, eles tem a mesma orientação (ou sempre a esquerda, ou sempre à direita).
// Definição da classe Point
// Implementação da função de orientação D
class Polygon {
public:
// Membros e construtor
bool is_convex() const
{
vector<Point> vs(vertices);
if (n < 3)
return false;
vs.push_back(vs[1]); // Temporário/inserção evitam um if no laço
int orientation = 0, i;
for (i = 0; i < n; ++i)
{
int d = D(vs[i], vs[i + 1], vs[i + 2]);
if (d == 0)
continue;
orientation = d;
break;
}
for (; i < n; ++i)
{
int d = D(vs[i], vs[i + 1], vs[i + 2]);
if (d == -orientation)
return false;
}
return orientation != 0;
}
};Para se verificar se um ponto P está localizado, ou não, no interior de um polígono, basta computar a soma dos ângulos formados por P e dois vértices do polígono (somando-se se o ponto está na mesma orientação do polígono, subtraíndo em caso contrário): se a soma totalizar 2PI, o ponto está no interior do polígono. Esta verificação vale tanto para polígonos convexos quanto côncavos.
// Definição da classe Point
// Definição de PI, da função equals() do discriminante D()
// Ângulo APB, em radianos
double angle(const Point& P, const Point& A, const Point& B)
{
auto ux = P.x - A.x;
auto uy = P.y - A.y;
auto vx = P.x - B.x;
auto vy = P.y - B.y;
auto num = ux * vx + uy * vy;
auto den = hypot(ux, uy) * hypot(vx, vy);
// Caso especial: se den == 0, algum dos vetores é degenerado: os dois
// pontos são iguais. Neste caso, o ângulo não está definido
return acos(num / den);
}
class Polygon {
public:
// Membros e construtores
bool contains(const Point& P) const
{
if (n < 3)
return false;
auto sum = 0.0;
for (int i = 0; i < n; ++i)
{
auto d = D(P, vertices[i], vertices[i + 1]);
// Pontos sobre as arestas ou vértices são considerados interiores
if (equals(d, 0))
return true;
auto a = angle(P, vertices[i], vertices[i + 1]);
sum += d > 0 ? a : -a;
}
return equals(fabs(sum), 2*PI);
}
};Dada uma reta r, que passa pelos pontos A e B, e um polígono convexo P, com n vértices, esta reta secciona o polígono em duas regiões, esquerda e direita, que podem ser ou uma vazias e outra contendo P integralmente, ou serem compostas de dois polígonos convexos P1 e P2, resultantes do corte de P por r.
A rotina cut_polygon(), apresentada abaixo e adaptada de
Competitive Programming 3, retorna a região a esquerda
do corte, considerando que P está descrito no sentido anti-horário.
// Definição da classe Point, da função equals() e do discriminante D()
// Interseção entre a reta AB e o segmento de reta PQ
Point intersection(const Point& P, const Point& Q, const Point& A, const Point& B)
{
auto a = B.y - A.y;
auto b = A.x - B.x;
auto c = B.x * A.y - A.x * B.y;
auto u = fabs(a * P.x + b * P.y + c);
auto v = fabs(a * Q.x + b * Q.y + c);
return Point((P.x * v + Q.x * u)/(u + v), (P.y * v + Q.y * u)/(u + v));
}
Polygon cut_polygon(const Polygon& P, const Point& A, const Point& B)
{
vector<Point> points;
for (int i = 0; i < P.n; ++i)
{
auto d1 = D(A, B, P.vertices[i]);
auto d2 = D(A, B, P.vertices[i + 1]);
// Vértice à esquerda da reta
if (d1 > -EPS)
points.push_back(P.vertices[i]);
// A aresta cruza a reta
if (d1 * d2 < -EPS)
points.push_back(intersection(P.vertices[i], P.vertices[i+1], A, B));
}
return Polygon(points);
}
Um polígono regular (isto é, com lados de medidas iguais) de n lados possui um círculo circunscrito (cujos vértices do polígono pertencem ao círculo) e um círculo inscrito (cujos lados são tangentes ao círculo).
O raio R do círculo circunscrito é igual ao raio do polígono: a distância entre o seu centro e um de seus vértices. A área do polígono pode então ser computada a partir de R e de n, através da expressão dada abaixo.
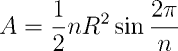
// Definição da constante PI
// Área do polígono regular de n lados inscrito no círculo de raio R
double area(double R, int n)
{
return 0.5*n*R*R*sin(2*PI/n);
}O raio r do círculo inscrito pode ser determinado a partir da medida s de um dos lados do polígono regular, através da relação abaixo,
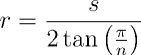
ou a partir do raio R do círculo circunscrito e n, pela relação dada a seguir.
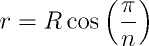
Dado um conjunto de pontos P, o envoltório convexo CH(P) de P (convex hull) é o menor polígono convexo tal que cada ponto de P ou pertence ao interior de CH(P) ou é um de seus vértices.
Existem vários algoritmos para se determinar o envoltório convexo, e como os vértices de CH(P) são pontos de P, a essência dos algoritmos é determinar, para cada ponto de P, se ele pertence ou não ao CH(P).
O algoritmo de Graham iniciamente ordena todos os n pontos de P de acordo com o ângulo que eles fazem com um ponto pivô fixado previamente. A escolha padrão para o pivô é o ponto de menor coordenada y e, caso exista mais de um ponto com coordenada y mínima, escolhe-se o de maior coordenada x dentre eles. Para simplificar o algoritmo, o pivô é movido para a primeira posição do vetor.
// Definição da classe Point
Point pivot(vector<Point>& P)
{
size_t idx = 0;
for (size_t i = 1; i < P.size(); ++i)
if (P[i].y < P[idx].y or (equals(P[i].y, P[idx].y) and P[i].x > P[idx].x))
idx = i;
swap(P[0], P[idx]);
return P[0];
}Para realizar a ordenação, é preciso definir um operador booleano que receba dois pontos p e q e retorne verdadeiro se p antecede q de acordo com a ordenação proposta. Como é necessário o conhecimento do pivô para tal ordenação, há três possibilidades para a implementação deste operador:
- implementar o operator
<da classePoint, tornando o pivô um membro da classe, para que o operador tenha acesso a ele; - tornar o pivô uma variável global;
- usar uma função lambda no terceiro parâmetro da ordenação, capturando o pivô por referência ou cópia.
Abaixo segue um código que implementa a terceira estratégia.
// Definição da classe Point e do discriminante D()
// Definição da função pivot()
void sort_by_angle(vector<Point>& P)
{
auto P0 = pivot(P);
sort(P.begin() + 1, P.end(), [&](const Point& A, const Point& B)
{
// Corner case: pontos colineares. Escolhe-se o mais próximo do pivô
if (equals(D(P0, A, B), 0))
return A.distance(P0) < B.distance(P0);
auto dx = A.x - P0.x;
auto dy = A.y - P0.y;
auto alfa = atan2(dy, dx);
dx = B.x - P0.x;
dy = B.y - P0.y;
auto beta = atan2(dy, dx);
return alfa < beta;
}
);
}Com os pontos ordenados, o algoritmo procede da seguinte forma: ele empilha três pontos de P (inicialmente, os índices n -1, 0, 1) e mantem a invariante de que os três elementos do topo de pilha estão sempre em sentido anti-horário (D() > 0). Para cada um dos pontos de P, verifica-se se este ponto mantem o sentido anti-horário com os dois elementos do topo da pilha: se sim, o ponto é inserido na pilha e segue-se adiante; caso contrário, remove-se o topo da pilha e se verifica o invariante novamente. Como cada ponto é ou inserido ou removido uma única vez, este processo tem complexidade O(n), e o algoritmo como um todo tem complexidade O(nlog n), por conta da ordenação.
// Definição da classe Point e da função sort_by_angle()
Polygon convex_hull(const vector<Point>& points)
{
vector<Point> P(points);
auto n = P.size();
// Corner case: com 3 vértices ou menos, P é o próprio convex hull
if (n <= 3)
return Polygon(P);
sort_by_angle(P);
vector<Point> s;
s.push_back(P[n - 1]);
s.push_back(P[0]);
s.push_back(P[1]);
size_t i = 2;
while (i < n)
{
auto j = s.size() - 1;
if (D(s[j - 1], s[j], P[i]) > 0)
s.push_back(P[i++]);
else
s.pop_back();
}
if (s.front() == s.back())
s.pop_back();
return Polygon(s);
}Outros algoritmos para o envoltório convexo são o Andrew's Monotone Chain
Algorithm e o algoritmo Jarvis's March. Abaixo segue uma implementação
da cadeia monótona. Os pontos devem ser ordenados pela menor coordenada
x e, em caso de empate, pela menor coordenada y.
class Point {
public:
ll x;
ll y;
Point(ll xv = 0, ll yv = 0) : x(xv), y(yv) {}
bool operator<(const Point& P) const
{
return x == P.x ? y < P.y : x < P.x;
}
};
ll D(const Point& P, const Point& Q, const Point& R)
{
return (P.x * Q.y + P.y * R.x + Q.x * R.y) - (R.x * Q.y + R.y * P.x + Q.x * P.y);
}
vector<Point> monotone_chain_ch(vector<Point>& P)
{
sort(P.begin(), P.end());
vector<Point> L, U;
for (auto p : P)
{
while (L.size() >= 2 and D(L[L.size() - 2], L[L.size() -1], p) < 0)
L.pop_back();
L.push_back(p);
}
reverse(P.begin(), P.end());
for (auto p : P)
{
while (U.size() >= 2 and D(U[U.size() - 2], U[U.size() -1], p) < 0)
U.pop_back();
U.push_back(p);
}
L.pop_back();
U.pop_back();
L.reserve(L.size() + U.size());
L.insert(L.end(), U.begin(), U.end());
return L;
}
- Codeforces
- UVA
HALIM, Steve; HALIM, Felix. Competitive Programming 3, Lulu, 2013.
Math Open Reference. Incircle of a Polygon. Acesso em 18/08/2016.
Mathwords. Area of a Regular Polygon. Acesso em 20/09/2016.
Wikipédia. Regular Polygon. Acesso em 18/08/2016.