-
Notifications
You must be signed in to change notification settings - Fork 153
Pontos
Os pontos são elementos básicos da geometria, e são elementos adimensionais (dimensão 0). A maioria dos outros elementos e definições da geometria se referem a pontos, e o termo ponto, em si, é um termo primitivo (sem definição).
Na prática, em C/C++, um ponto pode ser representado de várias maneiras, cada uma com suas respectivas vantagens e desvantagens:
-
structouclassRepresentar um ponto utilizando uma classe ou estrutura tem a vantagem da legibilidade, mas precisa da implementação dos operadores relacionais para comparações entre pontos.
typedef struct _Point { double x; double y; } Point;
...
Point p, q; // Declaração p.x = 5; q.y = 10;
p = q; // Atribuição
if (p < q) { // Erro de compilação: operador < não definido! ... } ```
Nestas representações, é útil definir construtores para a inicialização
das variáveis.
```C++
class Point { public: double x; double y;
Point(double xv = 0, double yv = 0) : x(xv), y(yv) {}
};
...
Point p(5), q(0, 10); // Exemplos de uso do construtor (p = (5, 0)) ```
-
std::pairUsar pares do C++ tem a vantagem de herdar os operadores de comparação dos tipos definidos. Porém, a desvantagem é a notação, que utiliza
firstesecondao invés dexey, sendo menos legível que o uso de classes e estruturas. Além disso, não podem ser utilizados diretamente para representar pontos tridimensionais.
using point = pair<double, double>; // C++11
...
point p, q; // Declaração p.first = 5; q.second = 10;
p = q; // Atribuição
if (p < q) { // Ok! Operador < para doubles utilizado ... } ```
A desvantagem de notação menos legível pode ser contornada com o uso
de macros, conforme mostrado abaixo.
```C++
#define x first
#define y second
```
Contudo, ao usar tais macros, deve-se tomar cuidado pois todas as aparições
de x e `y` serão substituídas por `first` e `second`. Logo a declaração de
uma variável com nome `x` pode levar a um erro de compilação.
-
arrays
Utilizar arrays para representar pontos permite a representação de conjuntos de pontos com facilidade, além de permitir a travessia via laço
forpor coordenada. Porém, peca na legibilidade (índices inteiros para acesso aos membros) e na necessidade de definição dos operadores.
double p[2], q[2]; // Declaração usando arrays unidimensionais de tamanho 2 p[0] = 5; q[1] = 10;
p = q; // Erro de compilação: operador = não definido!
if (p < q) { // Perigo: comparação entre os endereços dos ponteiros! O ... // código compila normalmente! } ```
Caso a representação para pontos escolhida não herde os comparadores padrão do
C++, é necessário escrever os mesmos para a representação escolhida. Mesmo no
caso do uso de pares, é necessário escrever ao menos o operador de comparação,
para que o mesmo utilize o limiar  (EPS).
(EPS).
Abaixo segue um exemplo de implementação do operador de igualdade:
// Definição da função equals()
bool operator==(const point& a, const point& b)
{
return equals(a.first, b.first) && equals(a.second, b.second);
}A implementação do operador < é dada a seguir. Os demais operadores podem ser
implementados de forma semelhante.
// Definição do limiar EPS
typedef struct _Point {
double x;
double y;
} Point;
bool operator<(const Point& p, const Point& q)
{
return (equals(p.x,q.x)) ? (q.y - p.y) > EPS : q.x - p.x > EPS);
}
Observe que a comparação acima é feita coordenada a coordenada. Em certas situações, pode ser necessário ordenar pontos por sua distância a origem ou algum outro critério: se for o caso, basta alterar a implementação para o critério desejado.
A distância entre dois pontos pode ser computada utilizando o Teorema de Pitágoras: o quadrado da distância é igual a soma dos quadrados das diferenças entre as respectivas coordenadas (tanto em duas quanto três dimensões). Se as coordenadas forem inteiras, pode-se comparar o quadrado diretamente, sem a extração da raiz quadrada: isto permite a obtenção da igualdade sem o recurso do limiar, o que aumenta a velocidade e a precisão do cálculo.
typedef struct _Point {
double x;
double y;
double z;
} Point;
double distance(const Point& P, const Point& Q)
{
return sqrt((P.x - Q.x)*(P.x - Q.x) + (P.y - Q.y)*(P.y - Q.y) + (P.z - Q.z)*(P.z - Q.z));
}No caso bidimensional, o melhor é utilizar a função hypot da biblioteca
matemática padrão do C/C++: além de computar a distância corretamente, ela
trata de possíveis underflows ou overflows que possam vir a ocorrer
durante o cálculo.
using point = pair<double, double>;
point p, q;
...
auto dist = hypot(p.first - q.first, p.second - q.second); // #include <cmath>Um vetor pode se definido/entendido como um segmento de reta orientado. Embora os segmentos de reta sejam discutidos em maiores detalhes na seção Retas, vale destacar a relação entre pontos e vetores.
Dados dois pontos A e B, denotaremos AB o vetor que parte do ponto A em direção ao ponto B (observe que AB e BA tem mesma direção e comprimento, mas orientações distintas). O vetor posição de um ponto P é o vetor que une a origem O ao ponto P (OP).
Na prática, trabalha-se apenas com vetores-posição: o vetor posição
que corresponde ao vetor AB é o vetor v = (B.x - A.x, B.y - A.y). Deste
modo, embora seja possível definir um tipo de dado para representar vetores,
é possível utilizar pontos para representar vetores. Esta estratégia pode
dificultar a leitura das rotinas, há a vantagem da velocidade de codificação,
devido a redução de código semelhante. A título de ilustração, segue uma
possível implementação da classe Vector (não confundir com o contêiner
vector da STL).
// Definição da classe Point
class Vector {
public:
double x, y;
Vector(double xv, double yv) : x(xv), y(yv) {}
Vector(const Point& A, const Point& B) : x(B.x - A.x), y(B.y - A.y) {}
};O comprimento (ou magnitude) de um vetor é dado pela distância entre seus
pontos (no caso do vetor-posição, a distância do ponto até a origem). O ângulo
que o vetor faz com o eixo-x positivo pode ser determinado pelo arco tangente
da razão entre as coordenadas y e x. Vale ressaltar que a função atan (
que computa o arco tangente de um número) opera apenas no primeiro e quarto
quadrante do plano cartesiano (onde x > 0 e -π/2 ≤ θ ≤ π/2). Para superar
esta limitação, basta somar π ao retorno da função caso x < 0 (atenção ao
caso especial onde x = 0). Se o vetor for degenerado (isto é, liga a
origem à origem), o ângulo não estará definido (a função abaixo resultará em
-nan, isto é, not a number).
#define PI 3.141592653589793
class Vector {
public:
// Membros e construtores
double length() const
{
return hypot(x, y);
}
double angle() const
{
return atan(y / x) + (x < 0 ? PI : 0);
}
};Um ponto P pode ser transladado para outro ponto do espaço, conhecidos os deslocamentos dx, dy nas direções paralelas aos eixos-x e y, respectivamente (na verdade, a operação acontece no vetor posição correspondente).
// Definição da estrutura Point
Point translate(const Point& P, double dx, double dy)
{
return Point { P.x + dx, P.y + dy };
}Um ponto P pode ser rotacionado b graus radianos em torno da origem (0, 0), no sentido anti-horário, através da multiplicação do vetor posição v de P pela matriz de rotação R, dada abaixo.
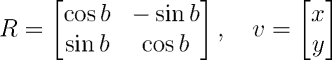
Esta matriz pode ser deduzida observando-se que as coordenadas do ponto podem
ser expressas como x = r cos a, y = r sin a (onde a é o ângulo que o vetor
v faz com o eixo-x e r é a magnitude de V) e
que as coordenadas do ponto resultante
da rotação são x' = r cos (a + b), y' = r sin (a + b).
O código abaixo ilustra esta rotação em linguagem C/C++.
// Definição da estrutura Point
Point rotate(const Point& P, double angle)
{
auto x = cos(angle) * P.x - sin(angle) * P.y;
auto y = sin(angle) * P.x + cos(angle) * P.y;
return Point { x, y };
}Caso se deseje rotacionar o ponto P em torno de outro ponto C que não seja a origem (mais precisamente, outro eixo paralelo a z que passe pelo ponto dado), basta seguir os três passos abaixo:
- Transladar o ponto com deslocamentos iguais aos opostos das coordenadas de C, obtendo-se P';
- Rotacionar o ponto transladado P';
- Transladar P', com deslocamentos iguais as coordenadas de C.
A translação inicial muda o sistema de coordenadas do problema, o levando a um novo sistema onde C é a origem. Assim, pode-se utilizar a rotina de rotação em torno da origem e, ao final do processo, retornar ao sistema original, com a translação inversa. Importante notar que as três operações devem ser realizadas exatamente na ordem descrita.
// Definição da classe Point e das funções translate() e rotate()
Point rotate(const Point& P, double angle, const Point& C)
{
auto Q = translate(P, -C.x, -C.y);
Q = rotate(Q, angle);
Q = translate(Q, C.x, C.y);
return Q;
}}
O mesmo raciocínio se aplica em três dimensões: as matrizes de rotação Rx, Ry e Rz, que rotacionam, no sentido anti-horário, em torno dos eixos x, y e z, respectivamente, são dadas abaixo.
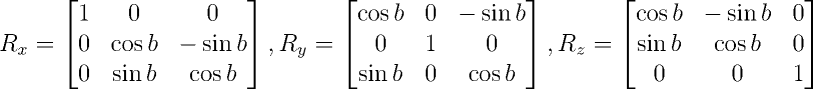
Dado um conjunto de pontos P, as operações de translação e rotação não alteram as distâncias entre os pares de pontos. Desta forma, se uma figura é descrita por um conjunto de pontos, todas as suas características que são baseadas em distâncias (ângulos internos, perímetro, área, volume, etc) são invariantes a estas duas transformações. Este importante fato pode ser utilizado para simplificar problemas, como foi feito no caso da rotação de torno de um ponto arbitrário.
Outra transformação possível em um ponto (vetor posição) é a escala, que consiste na multiplicação das coordenadas por um escalar. Se o mesmo escalar é utilizado em todos os produtos a escala é dita uniforme. Ao contrário das transformações anteriores, a escala não preserva as distâncias.
// Definição da classe Point
Point scale(double sx, double sy)
{
return Point(sx * P.x, sy * P.y);
}Uma aplicação comum da escala é a normalização de vetor. Um vetor é dito unitário se o seu comprimento é igual a 1. Dado um vetor v qualquer, é possível determinar um vetor unitário u, na mesma direção e sentido de v (a escala com constante positiva preserva direção e sentido), dividindo-se as coordenadas de v pelo comprimento de v.
// Definição da classe Vector
Vector normalize(const Vector& v)
{
auto len = v.length();
auto u = Vector(v.x / len, v.y / len);
return u;
}O produto interno entre dois vetores u e v é dado pela soma dos produtos das coordenadas correspondentes dos dois vetores. Logo, o resultado deste produto não é um vetor, e sim um escalar.
// Definição da classe Vector
double dot_product(const Vector& u, const Vector& v)
{
return u.x * v.x + u.y * v.y;
}É possível mostrar que este produto coincide com o produto do tamanho dos dois vetores e do cosseno do ângulo formado por estes vetores, conforme mostra a expressão abaixo.
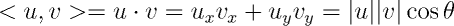
A relação acima nos permite computar o ângulo entre dois vetores.
// Definição da classe Vector e da função dot_product()
double angle(const Vector& u, const Vector& v)
{
auto lu = u.length();
auto lv = v.length();
auto prod = dot_product(u, v);
return acos(prod/(lu * lv));
}O sinal do produto interno d pode ser utilizado para interpretar a natureza do ângulo entre os dois vetores:
- se d == 0, os vetores são ortogonais (formam um ângulo de 90º);
- se d < 0, os vetores foram um ângulo agudo (menor que 90º);
- se d > 0, os vetores formam um ângulo obtuso (maior que 90º).
O produto vetorial entre dois vetores pode ser definido pelo vetor resultante do determinante abaixo, onde i, j, k são vetores unitários com mesma direção e sentido que os eixos x, y, z, respectivamente.
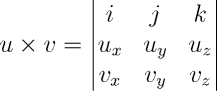
Veja que, definido como um determinante, o produto vetorial não é comutativo: a troca da ordem dos vetores altera o sentido do resultado. Para vetores bidimensionais, basta fazer a coordenada z = 0.
O vetor resultante é perpendicular tanto a u quanto a v, e pode-se mostrar que a magnitude deste vetor é igual ao produto dos comprimentos dos vetores u e v pelo seno do ângulo formado por estes dois vetores, o que coincide com a área do paralelogramo (ver seção Quadriláteros) formado por u e v.
// Definição da classe Vector
Vector cross_product(const Vector& u, const Vector& v)
{
auto x = u.y*v.z - v.y*u.z;
auto y = u.z*v.x - u.x*v.z;
auto z = u.x*v.y - u.y*v.x;
return Vector(x, y, z);
}Se os vetores tiverem mesma direção, o produto vetorial terá comprimento zero (como não definirão um plano, não há um vetor normal). Vetores normais podem ser utilizados para definir a orientação de uma figura tridimensional (o lado interno e externo da figura).
- UVA
HALIM, Steve; HALIM, Felix. Competitive Programming 3, Lulu, 2013.
STRANG, Gilbert. Introdução à Álgebra Linear, 4ª edição, LTC, 2013.