-
Notifications
You must be signed in to change notification settings - Fork 153
Retas
As retas são elementos unidimensionais da geometria e, assim como a palavra ponto, reta também é um termo primitivo da geometria.
Existem duas representações principais da reta: a equação reduzida e a equação geral. A equação reduzida de uma reta é a mais conhecida e utilizada nos cursos de ensino médio, e tem a vantagem de facilitar comparações entre retas e identificar paralelismo; porém não é capaz de representar retas verticais. A equação geral, como o próprio nome diz, pode representar qualquer reta do plano.
A equação reduzida da reta tem a forma y = mx + b, onde m é o coeficiente angular da reta e b é o coeficiente linear da reta. O primeiro coeficiente representa a variação da reta: consiste no número de unidades que y varia para cada unidade de variação de x no sentido positivo do eixo horizontal. O segundo coeficiente é o valor no qual a reta intercepta o eixo y.
Baseado na equação reduzida da reta, pode-se representar uma reta, em C/C++, utilizando-se uma classe ou estrutura da seguinte forma:
class Line {
public:
double m;
double b;
Line(double mv, double bv) : m(mv), b(bv) {}
};Conforme dito anteriormente, esta representação não permite a representação de retas verticais. Tal limitação pode ser contornada através do uso de uma variável booleana, que indica se a reta é ou não vertical. Em caso afirmativo, o coeficiente b passa a ser interpretado como o valor no qual a reta intercepta o eixo x.
class Line {
public:
double m;
double b;
bool vertical;
Line(double mv, double bv, bool v = false) : m(mv), b(bv), vertical(v) {}
};Dados dois pontos P = (x1, y1) e Q = (x2, y2), com x1 != x2, temos m = (y2 - y1)/(x2 - x1) e pode-se verificar que a reta que passa por P e Q tem equação reduzida y = m(x - x1) + y1.
// Definição da classe Point
class Line {
public:
double m;
double b;
bool vertical;
Line(double mv, double bv, bool v = false) : m(mv), b(bv), vertical(v) {}
Line(const Point& p, const Point& q)
{
if (equals(p.x, q.x)) // Reta vertical
{
b = p.x;
vertical = true;
} else
{
m = (p.y - q.y) / (p.x - q.x);
b = p.y - p.x * m;
vertical = false;
}
}
};A equação geral da reta tem a forma ax + by + c = 0 e, como dito, pode representar retas verticais (onde b = 0). Nos demais casos, é possível obter a equação reduzida a partir da equação geral.
class Line {
public:
double a;
double b;
double c;
Line(double av, double bv, double cv) : a(av), b(bv), c(cv) {}
};Dados dois pontos P = (x1, y1) e Q = (x2, y2), o coeficiente c pode ser obtido pela substituição direta das coordenadas de um dos dois pontos na equação geral. Conhecido o valor de c, pode-se obter os outros dois coeficientes resolvendo um sistema linear, cujas equações são resultante das substituições das coordenadas dos dois pontos.
Contudo, este processo pode ser simplificado com o uso de Álgebra Linear: se três pontos P = (x1, y1), Q = (x2, y2) e R = (x, y) são colineares (isto é, pertencem a uma mesma reta), então o determinante abaixo se anula.
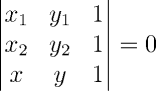
Desta forma, temos a = y1 - y2, b = x2 - x1, c = x1y2 - x2y1. Importante notar que este determinante, além de permitir a identificação dos coeficientes da equação geral da reta, pode ser utilizado para determinar outras relações, conforme será explicado mais adiante.
// Definição da classe Point
class Line {
public:
double a;
double b;
double c;
Line(double av, double bv, double cv) : a(av), b(bv), c(cv) {}
Line(const Point& p, const Point& q)
{
a = p.y - q.y;
b = q.x - p.x;
c = p.x * q.y - p.y * q.x;
}
};Um mesma reta pode ter infinitas equações gerais associadas: basta multiplicar toda a equação por uma número real diferente de zero. Para normalizar a representação, associando uma única equação a cada reta, é necessário dividir toda a equação pelo coeficiente a (ou por b, caso a seja igual a zero). Esta estratégia permite a simplificação de algoritmos de comparação entre retas.
// Definição da classe Point
class Line {
public:
double a;
double b;
double c;
Line(double av, double bv, double cv) : a(av), b(bv), c(cv) {}
Line(const Point& p, const Point& q)
{
a = p.y - q.y;
b = q.x - p.x;
c = p.x * q.y - p.y * q.x;
auto k = a ? a : b;
a /= k;
b /= k;
c /= k;
}
};Importante notar que, em ambas representações, pode acontecer da reta resultante ser degenerada. Isto ocorre quando os pontos p e q são idênticos: neste caso, a reta se reduz a um único ponto. O tratamento deste caso especiais nos demais algoritmos aumenta o tamanho e complexidade dos códigos. Dado o aspecto didático deste material, este caso será ignorado deste ponto em diante, mas o leitor é incentivado a tratá-lo em seus códigos.
Em relação às possíveis interseções entre duas retas, há três cenários possíveis: nenhum ponto em comum, um único ponto em comum ou todos os pontos em comum. No primeiro caso as retas são ditas paralelas; no segundo caso, concorrentes; no último, coincidentes.
O coeficiente angular é a chave para tal classificação: retas com coeficientes angulares distintos são concorrentes. Na coincidência destes concorrentes, é necessário verificar também o coeficiente linear: se iguais, as retas são coincidentes. Retas com coeficientes angulares iguais e coeficientes lineares distintos são paralelas.
A implementação destas verificações é trivial na representação baseada na equação reduzida, sendo necessário apenas o cuidado no trato do caso das retas verticais.
// Definição da função equals()
class Line {
public:
// Membros e construtores
bool operator==(const Line& r) const // Verdadeiro se coincidentes
{
if (vertical != r.vertical || !equals(m, r.m))
return false;
return equals(b, r.b);
}
bool parallel(const Line& r) const // Verdadeiro se paralelas
{
if (vertical and r.vertical)
return b != r.b;
if (vertical or r.vertical)
return false;
return equals(m, r.m) && !equals(b, r.b);
}
};No caso da representação baseada na equação geral da reta com coeficientes normalizados, para checar se retas são paralelas (ou coincidentes) basta comparar os coeficientes da reta.
// Definição da função equals
class Line {
public:
// Membros e construtores de uma reta baseada na equação geral com
// coeficientes normalizados
bool operator==(const Line& r) const
{
return equals(a, r.a) && equals(b, r.b) && equals(c, r.c);
}
bool parallel(const Line& r) const
{
return equals(a, r.a) && equals(b, r.b) && !equals(c, r.c);
}
};Duas retas serão perpendiculares se o produto de seus coeficientes angulares for igual a -1.
// Definição da função equals()
class Line {
public:
// Membros e construtores, equação reduzida
bool orthogonal(const Line& r) const // Verdadeiro se perpendiculares
{
if (vertical and r.vertical)
return false;
if ((vertical && equals(r.m, 0)) || (equals(m, 0) && r.vertical))
return true;
if (vertical or r.vertical)
return false;
return equals(m * r.m, -1.0);
}
};Outra maneira de checar se duas retas são perpendiculares é escolher dois pontos pertencentes a cada reta e montar dois vetores u e v cujas coordenadas são a diferença entre as coordenadas dos pontos escolhidos. Se o produto interno dos dois vetores for igual a zero, as retas são perpendiculares.
Importante notar, porém, é que os coeficientes a, b da equação geral de uma reta formam um vetor v = (a, b) perpendicular à reta. Tais vetores, denominados normais, podem ser utilizados na comparação descrita no parágrafo anterior.
// Definição da função equals()
class Line {
public:
// Membros e construtores, equação geral
bool orthogonal(const Line& r) const
{
return equals(a * r.a + b * r.b, 0);
}
};Como dito anteriormente, dado um par de retas, elas podem ser coincidentes (infinitas interseções), paralelas (nenhuma interseção) ou concorrentes (um único ponto de interseção).
Para encontrar o ponto de interseção, no caso de retas concorrentes, basta resolver o sistema linear resultante das equações gerais das duas retas.
// Definição função equals()
// Definições das classes Point e Line
#define INF -1
pair<int, Point> intersections(const Line& r, const Line& s)
{
auto det = r.a * s.b - r.b * s.a;
if (equals(det, 0))
{
// Coincidentes ou paralelas
int qtd = (r == s) ? INF : 0;
return pair<int, Point>(qtd, Point());
} else
{
// Concorrentes
auto x = (-r.c * s.b + s.c * r.b) / det;
auto y = (-s.c * r.a + r.c * s.a) / det;
return pair<int, Point>(1, Point(x, y));
}
}Para mensurar o ângulo formado por duas retas (ou dois segmentos de reta), é preciso identificar os vetores u e v de direção das duas retas e usar o produto interno. Dados dois pontos P = (x1, y1) e Q = (x2, y2), o vetor direção da reta que passa por P e Q é dado por u = (x1 - x2, y1 - y2).
De posse dos vetores de direção, o cosseno ângulo entre as retas é dado pela expressão abaixo:
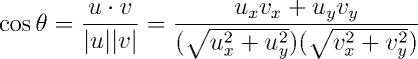
Para achar o ângulo, basta computar a função inversa do cosseno (acos, na
biblioteca de matemática padrão do C/C++) no lado direito da expressão acima.
// Definição da classe Point
// Ângulo entre os segmentos de reta PQ e RS
double angle(const Point& P, const Point& Q, const Point& R, const Point& S)
{
auto ux = P.x - Q.x;
auto uy = P.y - Q.y;
auto vx = R.x - S.x;
auto vy = R.y - S.y;
auto num = ux * vx + uy * vy;
auto den = hypot(ux, uy) * hypot(vx, vy);
// Caso especial: se den == 0, algum dos vetores é degenerado: os dois
// pontos são iguais. Neste caso, o ângulo não está definido
return acos(num / den);
}A distância de um ponto P a uma reta r é definida como a menor distância possível entre todos os pontos de r e P. Contudo, não é necessário computar estas infinitas distâncias possíveis: a menor distância será aquela entre P e o ponto de interseção Q de r com a reta perpendicular a r que passa por P.
Seja usando álgebra, geometria ou álgebra linear, é possível mostrar que esta distância d entre P = (x0, y0) e a reta ax + by + c = 0 é dada por
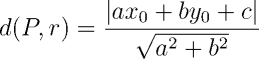
As coordenadas de Q = (x1, y1) podem ser obtidas utilizando-se as expressões abaixo
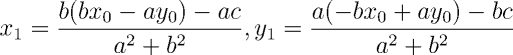
Abaixo temos a implementação da distância e do ponto mais próximo em C++.
// Definição da classe Point
class Line {
public:
// Membros e construtores
double distance(const Point& p) const
{
return fabs(a*p.x + b*p.y + c)/hypot(a, b);
}
Point closest(const Point& p) const // Ponto da reta mais próximo de p
{
auto den = a*a + b*b;
auto x = (b*(b*p.x - a*p.y) - a*c)/den;
auto y = (a*(-b*p.x + a*p.y) - b*c)/den;
return Point(x, y);
}
};Dado o segmento de reta PQ, a mediatriz é a reta perpendicular a PQ que passa pelo ponto médio do segmento. Qualquer ponto da reta mediatriz é equidistante de P e Q, e esta propriedade permite a dedução dos coeficientes a, b, c da mediatriz.
// Definição das classes Point e Line
Line perpendicular_bisector(const Point& P, const Point& Q)
{
auto a = 2*(Q.x - P.x);
auto b = 2*(Q.y - P.y);
auto c = (P.x * P.x + P.y * P.y) - (Q.x * Q.x + Q.y * Q.y);
return Line(a, b, c);
}Conforme dito anteriormente, o determinante utilizado para o cálculo dos coeficientes da equação geral da reta também identifica a orientação de um ponto em relação a uma reta. Se r é uma reta que passa pelos pontos P e Q, e R é um ponto qualquer, o determinante abaixo permite identificar se o ponto R pertence a reta (D = 0), ou está no semiplano à esquerda (D > 0) ou no semiplano à direita (D < 0). A orientação (esquerda ou direita) diz respeito à direção que vai de P a Q.
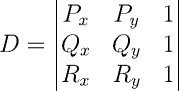
// Definição da classe Point
// D = 0: R pertence a reta PQ
// D > 0: R à esquerda da reta PQ
// D < 0: R à direita da reta PQ
double D(const Point& P, const Point& Q, const Point& R)
{
return (P.x * Q.y + P.y * R.x + Q.x * R.y) - (R.x * Q.y + R.y * P.x + Q.x * P.y);
}
Um segmento de reta é uma seção finita de uma reta r, delimitada por dois pontos A e B pertencentes a r. Um segmento de reta pode ser representado justamente por estes dois pontos, e o comprimento do segmento será igual a distância entre estes pontos.
// Definição da classe Point
class Segment {
public:
Point A, B;
Segment(const Point& Av, const Point& Bv) : A(Av), B(Bv) {}
double length() const
{
return hypot(A.x - B.x, A.y - B.y);
}
};Dois problemas, comuns entre pares de retas, requerem maior atenção quando envolvem segmentos de retas: ponto mais próximo do segmento e interseção entre dois segmentos de reta.
No primeiro problema, determinar o ponto do segmento AB mais próximo de um ponto P dado, é preciso avaliar também os extremos do segmento, pois o ponto Q mais próximo à reta r que contém AB pode estar fora do segmento. Assim, o ponto mais próximo (e a respectiva distância) será, dentre A, B e Q, o mais próximo de P que pertença ao intervalo.
// Definição das classes Point e Line
class Segment {
public:
// Membros e construtor
// Verifica se um ponto da reta _r_ que contém _A_ e _B_ pertence ao segmento
bool contains(const Point& P) const
{
if (equals(A.x, B.x))
return min(A.y, B.y) <= P.y and P.y <= max(A.y, B.y);
else
return min(A.x, B.x) <= P.x and P.x <= max(A.x, B.x);
}
// Ponto mais próximo de P no segmento
Point closest(const Point& P)
{
Line r(A, B);
auto Q = r.closest(P);
if (this->contains(Q))
return Q;
auto distA = P.distance(A);
auto distB = P.distance(B);
if (distA <= distB)
return A;
else
return B;
}
}A maneira mais comum de resolver o segundo problema, que consistem em determinar a interseção entre dois segmentos de reta, é resolver o problema para as duas retas que contém os respectivos segmentos e verificar se as interseções pertencem a ambos intervalos. Embora esta abordagem permita conhecer as coordenadas das possíveis interseções, ela traz alguns problemas em potencial:
- mesmo que as retas sejam coincidentes, não há garantias que os segmentos tenham interseção;
- a concorrência também não garante interseção: ainda é preciso verificar se o ponto pertence a ambos intervalos.
Se a questão fora apenas determinar se há ou não interseção, pode-se utilizar um algoritmo diferente, baseado no discriminante D. A ideia central é que dois segmentos se interceptam se a reta que passa por um segmento separa os dois pontos do outro segmento em semiplanos distintos. É preciso, contudo, tomar cuidado com o caso onde um dos pontos de um segmento é colinear ao pontos do outro segmento.
// Definição da classe Point e do discriminante D()
class Segment {
public:
// Membros e construtor
// Definição do método contains()
bool intersect(const Segment& s) const
{
auto d1 = D(A, B, s.A);
auto d2 = D(A, B, s.B);
if ((equals(d1, 0) && contains(s.A)) || (equals(d2, 0) && contains(s.B)))
return true;
auto d3 = D(s.A, s.B, A);
auto d4 = D(s.A, s.B, B);
if ((equals(d3, 0) && s.contains(A)) || (equals(d4, 0) && s.contains(B)))
return true;
return (d1 * d2 < 0) && (d3 * d4 < 0);
}
}Uma maneira de evitar um possível overflow no produto dos discriminantes é modificar a função D() para que retorne apenas o sinal do discriminante (0, -1 ou 1).
- UVA:
HALIM, Steve; HALIM, Felix. Competitive Programming 3, Lulu, 2013.
O'ROURKE, Joseph. Computational Geometry in C, 2nd edition, Cambridge University Press, 1998.
SKIENA, Steven S.; REVILLA, Miguel A. Programming Challenges: The Programming Contest Training Manual, Springer, 2002.
STRANG, Gilbert. Introdução à Álgebra Linear, 4ª edição, LTC, 2013.
Wikipédia. Distance from a point to a line, acesso em 13 de julho de 2016.